CUDA 入门

发表于 更新于 分类于 阅读次数：

…

CUDA

参考书：

  • CUDA C Programming Guide
  • CUDA Best Practice Guide

社区：
Cuda-zone

CUDA 基础

CPU 计算

现代CPU技术和架构都已经有了性能上的优化：流水线技术，分支预测，超标量，乱序执行，存储器层次，矢量操作，多核处理等。CPU内部包含多个核心，共享三级缓存，访存控制，外设接口等。

并行计算

并行计算的编程模型有：

  • 共享存储模型
  • 线程模型
  • 消息传递模型
  • 数据并行模型

GPU 开发环境搭建

Windows 安装

安装Visual Stuido与CUDA，搞深度学习还可以再安装CUDNN。

Visual Stuido 2019

CUDA

cuDNN（需要登录）

安装完成后，打开Visual Studio，新建项目，选择NVIDIA的CUDA项目，选择CUDA Runtime，输入项目名称，确定创建。

CUDA代码以.cu为后缀。创建完成后，软件自动打开kernel.cu文件。这是一个示例文件，可以在此基础上进行开发。按下Ctrl+F5编译运行程序。运行成功表名安装成功。

另外，CUDA会提供CUDA Samples，可以参考使用。

如果找不到cublas64_100.dll，可以去C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v10.2\bin下把下面的文件修改为所缺文件即可。

1
2
3
cublas64_10.dll
cusolver64_10.dll
cudart64_101.dll

Ubuntu 安装

查看系统相关信息：

1
2
3
4
5
6
7
8
# 查看系统版本
cat /etc/issue
# 查看显卡
lspci | grep -i nvidia
# Linux发行版本
uname -a
# 查看gcc
gcc -v

下载CUDA。

安装支持库：

1
sudo apt-get install freeglut3-dev build-essential libxll-dev libxmu-dev libxi-dev libgll-mesa-glx libglul-mesa-dev

卸载旧的NVIDIA驱动：

1
sudo nvidia-uninstall

清除相关的库：

1
sudo apt-get --purge remove nvidia-*
1
2
cd /etc/modprobe.d/
vim nvidia-installer-disable-nouveau.conf

文件内容是：

1
2
blacklist nouveau
options nouveau modeset=0

关闭窗口管理器

1
service lightdm stop

重启电脑。

安装CUDA：

1
2
3
4
5
6
7
sudo sh cuda_*.run 
# 安装过程配置选项
# 是否接受EULA：accept
# 是否安装图形加速驱动：yes
# 是否安装CUDA：yes
# 是否安装CUDA样例代码：yes
# CUDA样例代码路径：回车，保持默认

配置环境变量：

1
2
vim ~/.bash.rc
source ~/.bash.rc

.bash.rc内容为：

1
2
3
export CUDA=/usr/local/cuda-9.2
export PATH=$CUDA/bin:$PATH
export LD_LIBRARY_PATH=/usr/lib:$CUDA/lib64:$CUDA/lib:/lib:$LD_LIBRARY_PATH

查看版本信息：

1
nvcc --version

编译样例代码：

1
2
cd NVIDIA*_Samples
make

运行样例：

1
2
cd bin/x86_64/linux/release/
./vectorAddDrv

GPU 体系架构

处理器资源

thread：是CUDA中的最小单位，由一个CUDA Core执行。一个CUDA Core包含一个ALU，相应的register和local memory。

warp：以32个thread组成的一个单元。warp中所有线程并行的执行相同的指令。

block：由若干thread组成，以及一块shared memory，硬件上则是由一块SM（Streaming Multiprocessors）执行。需要注意的是，大部分thread只是逻辑上并行，并不是所有的thread可以在物理上同时执行。这就导致，同一个block中的线程可能会有不同步调。

grid：由若干个block构成，除此之外还包含global memory，texture memory等。一个grid由一个设备负责运行。

kernel：是在GPU上执行的一个程序。一个kernel启动一个grid，包含了若干线程块，这个数量可以由用户定义。每一个线程和线程块都有唯一的标识。

存储器资源

GPU的存储包括：
Register：片内，由thread私有。
Shared Memory：片内，属于block拥有。
Local Memory：片外，由thread私有。
Global Memory：片外，每个grid公用。
Constant Memory：片外。
Texture Memory：片外，对于主机可写，对于设备只读。
Instruction Memory：片外，不可见的。

CPU与GPU有各自的存储空间，二者通过PCI-E总线连接。因此在编程过程中，所有的数据必须预先传输给GPU，产生的结果也得通过总线取回。

编程模型

函数

在编程中，如果要将变量和函数放入GPU中执行，需要修饰关键字修饰相关的变量和函数。

函数声明：

1
2
3
4
5
6
// 执行位置：设备，调用位置：设备
__device__ float DeviceFunc()
// 执行位置：设备，调用位置：主机
__global__ void KernelFunc() 
// 执行位置：主机，调用位置：主机
__host__ float HostFunc()

其中__global__函数必须返回void，__device__与__host__可以同时使用。

由__global__修饰的函数又叫核函数（Kernels），调用核函数需要指定占用的线程数。

1
2
3
4
5
6
7
8
9
10
11
12
__global__ void VecAdd(float *A, float *B, float *C)
{
    int i = threadIdx.x;
    C[i] = A[i] + B[i];
}

int main()
{
    int A[100], B[100], C[100];
    // 1个Block，每个Block含32个Threads
    VecAdd<<<1, 32>>>(A, B, C);
}

在GPU上编写程序与在CPU上编写不同，在GPU上：

  • 不鼓励使用递归，因为其堆栈很小；
  • 不要使用静态变量；
  • 少用malloc，因为众多线程都去malloc，量就会很大；
  • 小心指针，尤其是函数指针。

Block可以使用一维，二维或三维方式访问Thread。

每一个线程都有一个编号：Thread Index。
对于一维Block，有：
Thread ID == Thread Index；
对于二维Block(Dx, Dy)，有：
Thread ID of index(x, y) == x + y * Dy；
对于三维Block(Dx, Dy, Dz)，有：
Thread ID of index(x, y, z) == x + y * Dy + z * Dx * Dy

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
__global__ void MatAdd(float A[N][N], float B[N][N], float C[N][N])
{
    // threadIdx -> Thread Index
    int i = threadIdx.x;
    int j = threadIdx.y;
    C[i][j] = A[i][j] + B[i][j];
}

int main()
{
    int numBlocks = 1;
    dim3 threadsPerBlock(N, N);
    // 1个Block，每个Block含 N * N 个Threads
    MatAdd<<<numBlocks, threadsPerblock>>>(A, B, C);
}

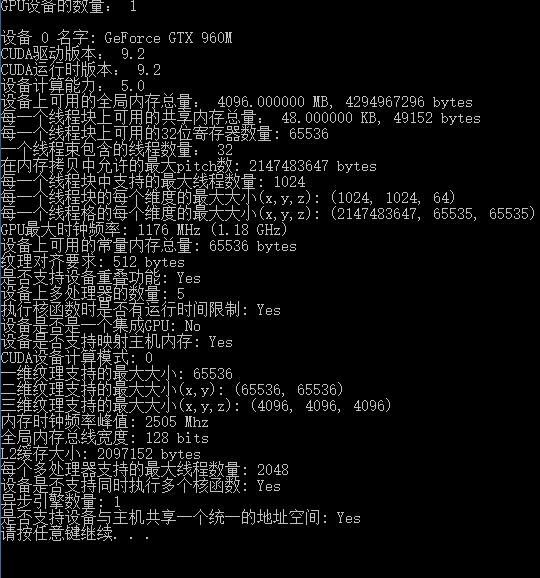
注意：最大线程数在不同的显卡中是不一样的，具体要看显卡的相关资料。如图所示，该显卡每个线程块最大含有1024个线程。

Grid可以用一维或多维的方式访问Block。

每一个块都有一个块索引：blockIdx。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
__global__ void MatAdd(float A[N][N], float B[N][N], float C[N][N])
{
    // threadIdx -> Thread Index
    // blockDim -> Block Dimension
    // blockIdx -> Block Index
    int i = blockIdx.x * blockDim.x + threadIdx.x;
    int j = blockIdx.y * blockDim.y + threadIdx.y;
    if (i < N && j < N){
        C[i][j] = A[i][j] + B[i][j];
    }
}

int main()
{
    dim3 threadsPerBlock(16, 16);
    dim3 numBlocks(N / threadsPerBlock.x, N / threadsPerBlock.y);
    MatAdd<<<numBlocks, threadsPerblock>>>(A, B, C);
}

例如，设N=32，那么Grid里面有2x2个Block：
blockIdx([0, 1], [0, 1])
blockDim = 16
threadIdx([0, 15], [0, 15])
i = [0, 1] * 16 + [0, 15]

访存

对于访存，不同的模型可以访问的内存区域也不同，读写属性也不同。

Register：由threads私有且可读可写，速度快，容量小。
Shared Memory：由block内的所有threads共享，且可读可写。
Local Memory：由threads私有且可读可写。
Global Memory：由grid内所有threads共享，可读可写；对于Host而言，也可读可写。
Constant Memory：由grid内所有threads共享，只可读；对于Host而言，可读可写。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 在设备端分配global memory
cudaMalloc()
// 释放存储空间
cudaFree()

// 例如：
float *Md;
int size = Width * Width * sizeof(float);
// 这里的Md是设备端的指针，不能在主机端使用
cudaMalloc((void**)&Md, size);
cudaFree(Md);

// 内存传输
cudaMemcpy(dest, src, size, direction);

// 例如：
cudaMemcpy(Md, M, size, cudaMemcpyHostToDevice);
cudaMemcpy(P, Pd, size, cudaMemcpyDeviceToHost);

方阵相乘示例 1

步骤：

  1. 分配内存，拷贝数据；
  2. 并行计算；
  3. 拷贝结果，释放内存。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

__global__ void MatrixMulKernel(float *M, float *N, float *P, int Width)
{
    // 获取当前计算的点 P(tx, ty)
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    float Pvalue = 0;

    // 矩阵相乘
    for (int k = 0; k < Width; k++){
        // 这里使用一维数组存储二维矩阵
        float Mdelement = Md[ty * Md.width + k];  
        float Ndelement = Nd[k * Nd.width + tx];
        Pvalue += Ndelement * Ndelement;
    }

    // 写回数据
    Pd[ty * Width + tx] = Pvalue;
}

void MatrixMulOnDevice(float *M, float *N, float *P, int Width)
{
    int size = Width * Width * sizeof(float);

    // 分配内存，拷贝数据
    cudaMalloc(Md, size);
    cudaMemcpy(Md, M, size, cudaMemcpyHostToDevice);
    cudaMalloc(Nd, size);
    cudaMemcpy(Nd, N, size, cudaMemcpyHostToDevice);
    cudaMalloc(Pd, size);

    // 并行计算 Width * Width 个线程
    dim3 dimBlock(Width, Width);
    dim3 dimGrid(1, 1);
    MatrixMulKernel<<<dimGrid, dimBlock>>>(Md, Nd, P, Width);

    // 拷贝结果，释放内存
    cudaMemcpy(P, Pd, size, cudaMemcpyDeviceToHost);
    cudaFree(Md);
    cudaFree(Nd);
    cudaFree(Pd);
}

但是这样的方式也有局限。首先是访存的频率和计算频率接近 1:1 ，而访存的时间又比较长，因此限制了性能。其次是每个Block限制了最大线程数，我们无法计算大型的矩阵乘法。

数据类型与操作

在GPU上支持向量数据类型，主要有：

  • char[1-4]
  • uchar[1-4]
  • short[1-4]
  • ushort[1-4]
  • int[1-4]
  • uint[1-4]
  • long[1-4]
  • ulong[1-4]
  • longlong[1-4]
  • ulonglong[1-4]
  • float[1-4]
  • double1
  • double2

他们同时适用于host和device，可以通过make_<typename>构造。例如

1
2
int2 i = make_int2(1, 2);
float4 f = make_float4(1.0f, 2.0f, 3.0f, 4.0f);

引用可以使用属性.x，.y，.z，.w的方式引用：

1
2
3
int2 i = make_int2(1, 2);
int x = i.x;
int y = i.y;

此外还有一些常用的数学函数：

  • sqrt
  • rsqrt
  • exp
  • log
  • sin
  • cos
  • tan
  • sincos
  • asin
  • acos
  • atan2
  • trunc
  • ceil
  • floor
  • 等

如果是在设备端，可以在对应函数前使用双下划线，如：__sin(x)，它的速度更快，但是精度较低。

块内线程同步

由于一个块内部的线程并不一定是同步的，有时又需要在特定的地方需要同步操作，因此可以使用同步函数。

1
__syncthreads();

该函数会等待所有线程完成任务再继续执行，但是同步也会造成死锁，编写代码的时候需要注意。

Wrap 线程束与线程调度

GPU执行程序时，是按照wrap为单位执行，一个wrap是32个线程。每一个wrap保证同一时刻下面的线程执行相同的指令（SIMD模式）。但是block下并不是只有32个线程，而是更多。因此一个block可以包含多个wrap，且wrap之间的程序不一定是同步的，而且甚至是一个wrap在执行，另外一个wrap在等待调度。

如果一个wrap下不同线程要经过不同的分支，又要保证同一时刻执行相同的指令，就要使用线程屏蔽技术。该技术使这32个线程在遇到分支结构时，例如程序进入分支1，那么就会屏蔽分支2的线程；等分支1执行完毕后，再屏蔽分支1，启动分支2的线程执行。

1
2
3
4
5
6
// 如果32个线程中既有满足分支1条件的线程，也有满足分支2条件的线程，那么就会按顺序，先执行分支1，再执行分支2，对于不满足条件的分支给予屏蔽。
if (condition){
    // 分支 1
}else{
    // 分支 2
}

对于一些老式显卡也有特殊情况。尽管调度是按照wrap为单位，但是承接调度的设备是一个SM。如果一个SM只能运行8个线程，那么此次调度的线程就要分4批进入SM，也就是32个线程就不会同步执行。对于现代显卡，一个SM基本上至少可以运行100多个线程。

内存模型

延时隐藏技术：在处理器处理程序时，处理的过程是很快的，但是当要进行访存等较慢且需要等待的操作，处理器就会停滞。为了让处理器“忙”起来，我们就会给处理器指派其他可以做的工作，直到前一次访存成功，再回去继续执行。

例如，有N个wrap，每个wrap访存一次需要16个周期，访存后停滞一段时间，每次访存只能有一个wrap。如果我们需要覆盖200个周期，那么需要的wrap数为：200 / 16 = 13个，才能掩藏延时。

另外，决定每个SM能够承载多少线程，是内部资源的分配决定的。

例如，每个SM含有8K个寄存器，当有768个线程需要分配时，每个线程可以分配8K / 768 = 10个寄存器。

再如，如果每个线程如果使用11个寄存器，那么这个SM就承载不了768个线程了。这样就会闲置CPU Core。

Local Memory是每个线程私有，但是存储在GPU的外存中。

Shared Memory是每个Block拥有，存储在GPU片内。它跟寄存器一样，也是决定SM能够承载多少线程的因素。

Global Memory可供全局使用，但是访问延时很长。

Constant Memory也可供全局使用，延时短，带宽高，容量有64KB，但是对于GPU只读。

声明内存可以使用：

声明 存储器 作用域 声明周期
单独的auto变量（非数组） register thread kernel
auto变量数组 local thread kernel
__shared__ int shared block kernel
__device__ int global grid application
__constant__ int constant grid application

Host可以通过如下的函数访问global和constant变量：

1
2
3
4
cudaGetSymbolAddress()
cudaGetSymbolSize()
cudaMemcpyToSymbol()
cudaMemcpyFromSymbol()

另外，constant变量必须在函数外声明。

方阵相乘示例 2

上一次的方阵相乘问题：

  • 仅使用一个block，线程数并不多，导致处理问题的规模受限制；
  • 有很多的global memory访存活动，占用较多的时间。

解决方案：

  1. 去除问题规模的限制：将结果矩阵拆分成小块，把一个小块布置到一个block中。
  2. 减少global memory访存：将需要的数据按小块读入shared memory。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

// 假设 1 个block最大包含16 * 16 = 256个线程
// 且shared memory足够使用
#define TILE_WIDTH  16

__global__ void MatrixMulKernel(float *M, float *N, float *P, int Width)
{
    // 创建shared memory
    __shared__ float Mds[TILE_WIDTH][TILE_WIDTH];
    __shared__ float Nds[TILE_WIDTH][TILE_WIDTH];

    int bx = blockIdx.x;
    int by = blockIdx.y;
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    // 获取当前计算的点 P(Row, Col)
    int Row = by * TILE_WIDTH + ty;
    int Col = bx * TILE_WIDTH + tx;

    float Pvalue = 0;

    // 矩阵相乘
    for (int k = 0; k < Width/TILE_WIDTH; k++){
        // 将数据从global memory读入shared memory
        Mds[ty][tx] = Md[Row * Width + (k * TILE_WIDTH + tx)]
        Nds[ty][tx] = Nd[Col + (k * TILE_WIDTH + ty) * Width]
        __syncthreads();
        // 当 Width/TILE_WIDTH 个小块全部读入数据到shared memory后，计算
        for (int m = 0; m < TILE_WIDTH; m++){
            Pvalue += Mds[ty][m] * Nds[m][tx];
        }
        __syncthreads();
    }

    // 写回数据
    Pd[Row * Width + Col] = Pvalue;
}

void MatrixMulOnDevice(float *M, float *N, float *P, int Width)
{
    
    int size = Width * Width * sizeof(float);

    // 分配内存，拷贝数据
    cudaMalloc(Md, size);
    cudaMemcpy(Md, M, size, cudaMemcpyHostToDevice);
    cudaMalloc(Nd, size);
    cudaMemcpy(Nd, N, size, cudaMemcpyHostToDevice);
    cudaMalloc(Pd, size);

    // 并行计算 Width * Width 个线程
    dim3 dimBlock(TILE_WIDTH, TILE_WIDTH);
    dim3 dimGrid(Width / TILE_WIDTH, Width / TILE_WIDTH);
    MatrixMulKernel<<<dimGrid, dimBlock>>>(Md, Nd, P, TILE_WIDTH);

    // 拷贝结果，释放内存
    cudaMemcpy(P, Pd, size, cudaMemcpyDeviceToHost);
    cudaFree(Md);
    cudaFree(Nd);
    cudaFree(Pd);
}

由于我们定义TILE_WIDTH为16，因此global memory的访存次数减少16倍。因为：

假设有两个16 * 16矩阵M，N相乘，则访存次数为16 * 16 * 32次，因为计算1个元素需要读取M的一行与N的一列，即32个元素参与计算，访存32次。

当使用shared memory后，我们访问global memory的次数为16 * 16 * 2次，也就是将2个16 * 16的矩阵复制到shared memory所需要的次数。

定义TILE_WIDTH大小应当根据：

  • 每个block所能容纳的线程数目；
  • 每个thread可以分配的Local Memory的大小；
  • 每个thread可以分配的Registry的数量；

原子操作

原子操作是耗时的，尽量少用原子操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
// 算术操作
atomicAdd()
atomicSub()
atomicExch()
atomicMin()
atomicMax()
atomicDec()
atomicCAS()

// 位运算
atomicAnd()
atomicOr()
atomicXor()

调试

使用Nsight可以调试：

Linux下可以使用命令：

1
nsight

打开Eclipse，编写一个CUDA程序。在设备代码中打入断点，Debug时即可在CUDA选项中查看变量的值，左侧可以选择CUDA线程。

提示：如果设备正在用于图像显示，则不能进行调试。

Nsight也可以进行性能分析，可以在Profiler中查看。

如果仅有一块GPU卡，需要先停止桌面环境，仅仅可以使用命令行调试，或从其他系统上通过Nsight远程调试。

程序优化

并行规约：例如有8个数据要求和，可以进行两两求和得到4个数据，再经过多次两两求和最终合并为1个数据。

合并的方式有两种，一种是：
第一轮：A[0] = A[0] + A[1]，A[2] = A[2] + A[3]，A[4] = A[4] + A[5]，A[6] = A[6] + A[7]；
第二轮：A[0] = A[0] + A[2]，A[4] = A[4] + A[6]；
第三轮：A[0] = A[0] + A[4]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
__global__ void SumOnDevice(float A[])
{
    __shared__ float partialSum[];
    // 载入数据到shared memory
    for (unsigned int k = 0; k < blockDim.x; k++){
        partialSum[k] = A[k];
    }
    // 求和
    unsigned int t = threadIdx.x;
    for(unsigned int stride = 1; stride < blockDim.x; stride *= 2){
        __syncthreads();
        if(t % (2 * stride) == 0){
            partialSum[t] += partialSum[t + stride];
        }
    }
}

另一种是：
第一轮：A[0] = A[0] + A[4]，A[1] = A[1] + A[5]，A[2] = A[2] + A[6]，A[3] = A[3] + A[7]；
第二轮：A[0] = A[0] + A[2]，A[1] = A[1] + A[3]；
第三轮：A[0] = A[0] + A[1]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
__global__ void SumOnDevice(float A[])
{
    __shared__ float partialSum[];
    // 载入数据到shared memory
    for (unsigned int k = 0; k < blockDim.x; k++){
        partialSum[k] = A[k];
    }
    // 求和
    unsigned int t = threadIdx.x;
    for(unsigned int stride = blockDim.x / 2; stride > 0; stride /= 2){
        __syncthreads();
        if(stride > t){
            partialSum[t] += partialSum[t + stride];
        }
    }
}

这两种方法是有区别的：

前者在进行第二轮运算时，会屏蔽1，3，5，7号线程，第三轮屏蔽1，2，3，5，6，7号线程，而留下1号与4号线程。这样就会使得每个wrap都被占用，但都只利用其中一小部分资源，从而造成资源的浪费。

后者则在第二轮减半后释放后面的4个线程，只留下前面的4个线程，可以减少占用的wrap数，而正在使用的wrap也得到了充分利用。

因此，我们在编写程序时，应当注意利用thread index与wrap的关系，合理的使用wrap。

thread index与wrap的关系，就是wrap 0对应031号线程；wrap 1对应3263号线程……以此类推。

存储优化

global memory

CPU与GPU数据传输应当减少传输，组团传输。应注意：

  • 中间数据直接在GPU上分配与释放；
  • GPU上更适合进行重复计算；
  • 如果没有减少数据传输，将CPU的的代码移植到GPU上也可能无法提示性能；
  • 大块传输要优于小块传输；
  • 采用双缓存同时计算与传输。

global memory的延迟很长，可以通过编译指令绕过一级缓存L1，只缓存于二级缓存L2。

1
-Xptxas - dlcm=cg

如果wrap的读写请求落到L1 cache line，则只需一次传输。因此应当使用合并原则，即使用连续的32字节块，对应一个wrap去处理，每个线程访问其中的1个字节。

另外，也尽量避免单个线程访问连续的字节块。

shared memory

shared memory的访问速度比global memory速度快上百倍，因此也可以使用shared memory缓存数据，再进行不规则访问。

shared memory被分为了许多banks（多体低位交叉存储），具备如下特性：

  • 连续的32bit（4字节）访存会被分配到连续的banks中；
  • 每个bank每周期可相应一个地址；
  • 多个bank也可以在同一个周期相应多个地址申请；
  • 如果对同一bank进行多次并发访存将导致bank冲突。

在没有bank冲突的情况下，share memory的存取速度几乎和register一样快。对于分析是否含有bank冲突，可以使用profiler分析器查看。

没有冲突的情况：

  • half-wrap内所有线程访问不同banks；
  • half-wrap内所有线程读取同一地址。

产生冲突的情况：

  • half-wrap内多个线程访问同一个bank；
  • 访存串行化。

矩阵转置

在矩阵转置中，不论是按行读按列写，还是按列读按行写，总有情况是访存不合并的。但是我们期望读写都是访存合并的。

这个问题可以通过shared memory解决。首先将小块数据由global memory读入shared memory，转置后再以连续化的数据写入global memory。这一过程中需要注意同步线程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
__global__ void transposeCoalesced(float *odata, float *idata, int width, int height)
{
    __shared__ float tile[TILE_DIM][TILE_DIM];

    int xIndex = blockIdx.x * TILE_DIM + threadIdx.x;
    int yIndex = blockIdx.y * TILE_DIM + threadIdx.y;
    int index_in = xIndex + yIndex * width;

    xIndex = blockIdx.y * TILE_DIM + threadIdx.x;
    yIndex = blockIdx.x * TILE_DIM + threadIdx.y;
    int index_out = xIndex + yIndex * height;

    // 下面会产生bank冲突
    tile[threadIdx.y][threadIdx.x] = idata[index_in];
    __syncthreads();
    odata[index_out] = tile[threadIdx.x][threadIdx.y];
}

由于这种方法会产生bank冲突，因此需要优化：tile[TILE_DIM][TILE_DIM]改为tile[TILE_DIM][TILE_DIM + 1]，也就是多一组用于占位，这样就不会连续多次访问同一个bank。

texure memory

texure memory对于GPU来说是一个只读存储器，其优势在于可以适应无法合并访存的场合，支持数据过滤输出（如：线性，双线性，三线性插值；由专用硬件完成），支持多维寻址，支持整数和小数作为坐标寻址，支持越界寻址。这些特征非常适用于对图像的处理。

SM 资源分割

SM上的资源是有限的，主要包含如下几类资源：

  • threads block slots：block 的最大值也受限制
  • threads slots
  • registers
  • shared memory

资源占用可以使用相应的计算器计算，CUDA GPU Occupancy Calculator。

循环展开

有时为了更好的性能，可以将循环展开：

1
2
3
4
5
for(i = 0; i < 16; i++){
    Sum += A[i];
}
// 改为
Sum += A[0] + A[2] + A[3] + A[4] + A[5] + A[6] ...

这一过程可以由编译器自动实现：

1
2
3
4
5
#pramga unroll BLOCK_SIZE
for(int i = 0; i < BLOCK_SIZE; i++){
    Sum += A[i];
}
#pramga

GPU 架构系列

系列命名：Tesla，Fermi，Kepler，Maxwell，Pascal，Volta，Turing，Ampere

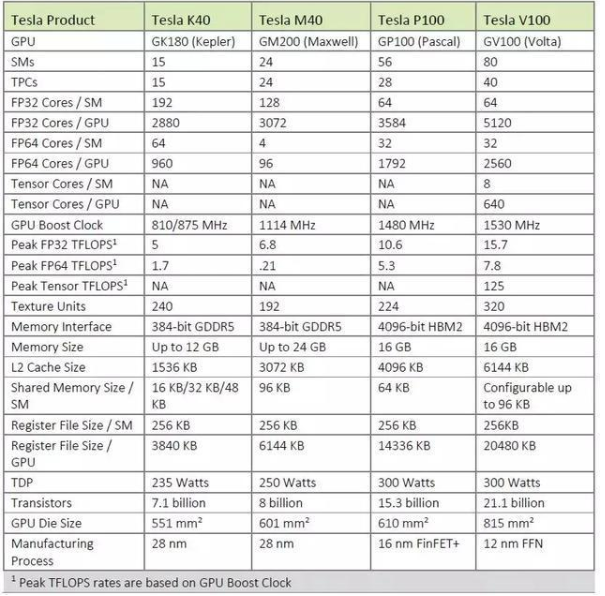
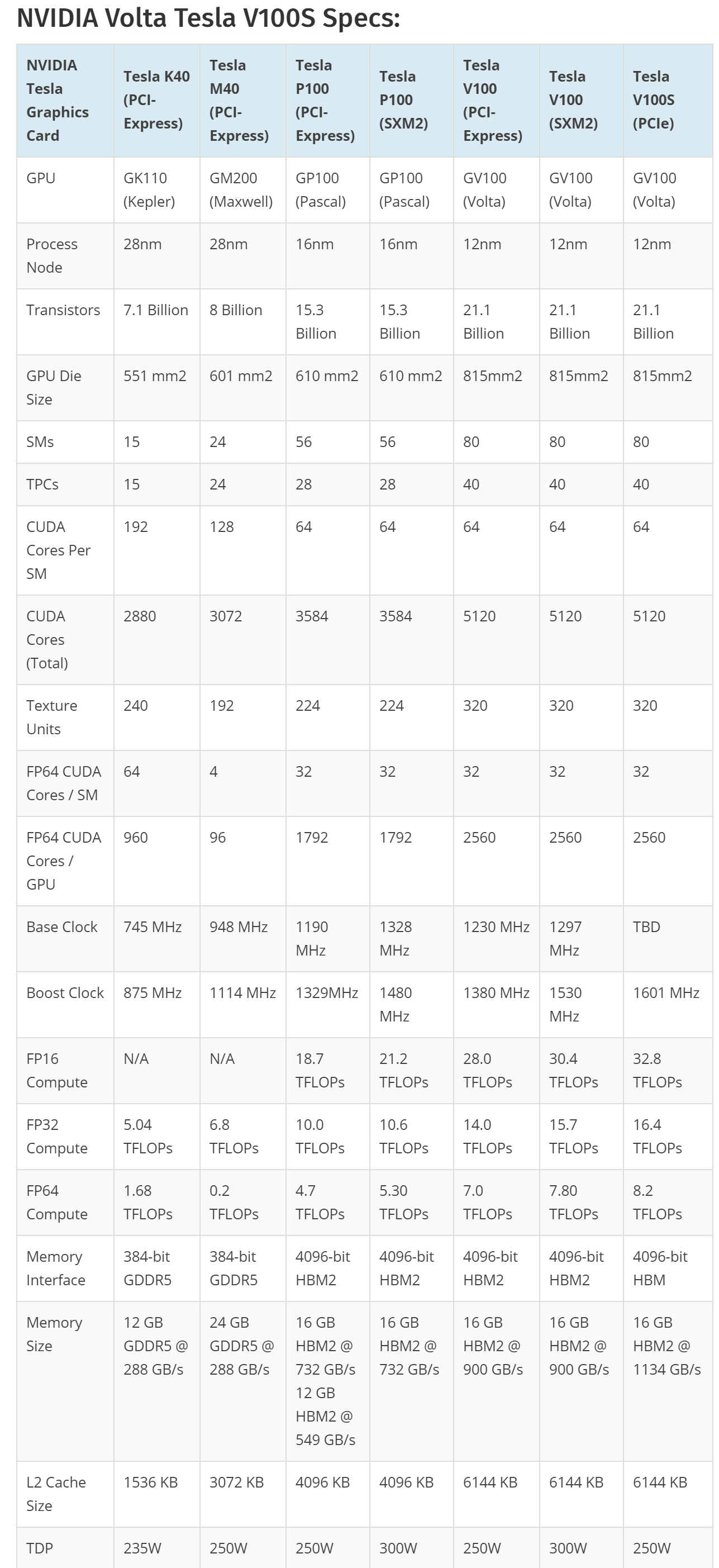
系列对比

Fermi 架构

Fermi是第一个完整的GPU计算架构，参考配置：

  • 16个SM，每个SM包含32个CUDA Core；
  • 每个CUDA Core包含1个ALU和1个FPU；
  • 6个384位GDDR5 DRAM，支持6GB global memory；
  • 768KB L2 Cache。

Fermi架构的部分显卡：GTX 480；GTX 470，GTX 465，GF 100等。

Kepler 架构

显卡：GTX600/600M系列和GTX700/700M系列。

特性：

  • Dynamic Parallelism：允许GPU动态的启动新的Grid。有了这个特性，任何kernel内都可以启动其它的kernel了。
  • Hyper-Q： 允许多个CPU核同时在单一GPU上启动线程，从而大大提高了GPU的利用率并削减了CPU空闲时间。
  • GPUDirect：能够使单个计算机内的GPU或位于网络内不同服务器内的GPU直接交换数据，无需进入CPU系统内存。
  • Grid Management Unit：能够使用先进、灵活的GRID管理和调度控制系统。

Maxwell 架构

显卡：GTX800/800M系列与GTX750和GTX750TI。

特性：加入了新的G-SYNC（垂直同步）技术。

Pascal 架构

显卡：

  • GeForce系列：GTX1050、1050Ti、1060(3G, 5G, 6G)、1070、1070Ti、1080、1080Ti等；
  • QUADRO系列：GP100、P6000、P5000、P4000、P2000、P1000、P600、P400等；
  • 特斯拉系列：P100、P4、P40；
  • TITAN XP。

CUDA API

API：