编译原理

发表于 2020-02-16 更新于 2024-06-07 分类于计算机理论阅读次数：

…

编译原理序章

翻译程序

$\sum_{i=0}^N\int_{a}^{b}g(t,i)\text{d}t$

编译程序是一种翻译程序，它是高级语言翻译为低级语言的过程，这个低级语言可以在计算机上运行。

编译程序有：

诊断编译程序
优化编译程序
交叉编译程序
可变目标编译程序

解释程序

把源语言写的源程序作为输入，但不产生目标程序，而是边编译边执行。

计算思维

计算思维就是计算机科学的思维方法：

抽象：提取一般过程；
自动化：将思维物化的过程；
问题分解：做全局性决策，再分解为小问题；
递归：通过解决子问题来解决大问题；
权衡：权衡理论与实际；
保护、冗余、容错、纠错、恢复
启发式推理
不确定情况下的规划、学习、调度

编译的五个过程：

词法分析：输入源程序，识别单词符号，遵循构词规则，利用有限自动机。
语法分析：根据单词符号串分解为语法单位，遵循语法规则，利用上下文无关文法。
中间代码产生：根据语法单位进行初步翻译，依据语义规则，利用属性文法。产生三元式，四元式，树。
优化：对中间代码优化，依据等价变换规则。
目标代码产生：变为目标代码，依据硬件系统结构和机器指令。有三种代码：汇编指令代码，绝对指令代码，可重定位指令代码（需要连接）。

编译程序的框架：

词法分析器
语法分析器
语义分析与中间代码生成器
优化段
目标代码生成器
符号表管理
出错处理：语法错误，语义错误。

高级语言

语法和语义和语用

语法：一组规则，用它可以形成和产生合适的程序。

词法规则：单词符号的形成规则。最基本结构。一般包括常数，标识符，基本字，算符，界符等。描述工具是有限自动机。

语法规则：语法单位的形成规则。一般包括表达式，语句，分程序，过程，函数，程序等。描述工具是上下文无关文法。

例如，E为表达式，i为标识符。下面表示一组构成表达式的语法规则：
E -> i
E -> E + E
E -> E * E
E -> (E)

语义：一组规则，可以定义一个程序的意义。

描述方法有：
- 自然语言描述：具有二义性，隐藏错误，不完整性；
- 形式描述：操作语义，指称语义，代数语义。

程序的层次：程序->子程序或函数->语句->表达式->运算符

高级语言分类：

强制式语言/过程式语言：一个语句接着一个语句强到对数据的操作。
应用式语言：强调描述函数的构造来实现对数据的处理。
基于规则的语言：检查一定条件，如果满足条件则执行动作。
面向对象语言：通过类，对象，消息与消息响应等处理数据。

程序结构：

FORTRAN：由主程序段和辅程序段构成。各段可独立编译。但是无法嵌套和递归。
PASCAL：可以看做是一个过程，允许嵌套和递归。
- 作用域
- 最近嵌套原则
JAVA：面向对象。

高级语言一般特性：

数据结构：
- 属性：区别于其他的对象的属性。
- 值：允许的取值。
- 操作：可以进行的操作。
数据类型与操作：
- 数值：
  - 整形，实数，复数，双精度
  - 加减乘除等
- 逻辑类型：
  - 布尔型
  - 布尔运算
- 字符类型：
  - 符号处理
- 指针类型

标识符：一种语法概念，由字母，数字组成。
名字：语义概念，标识程序中的对象。

标识符可以绑定到名字。

名字的意义和属性：

值：单元中的内容。
属性：类型和作用域。

名字的说明方式：

由说明语句来明确规定：如，int score
隐含说明：以某字母开头代表整形，否则为实数型
动态确定

数据结构：

数组：由同一类型的数据组成，分为可变与不可变长度。要给出访问方式，存放方式。
- 内情向量：登记维数，记录上下限等。
记录：元素构成，可各不相乘。各元素也称为域。要给出访问和存储方式。
字符串：符号处理，公式处理。
表格：记录结构
栈。
线性表。
抽象数据类型：由数据集合和相关操作组成，但操作不给出具体实现。

语句与控制结构：

表达式：操作数和算符组成
- 形式：前缀，后缀，中缀。
- 构成规则。
- 优先次序：左结合，右结合，代数性质（数学）。
语句：
- 赋值语句：
  - 名字的左值：该名字代表的地址。
  - 名字的右值：该名字代表的值。
- 控制语句：
  - 无条件转义。
  - 条件语句。
  - 循环语句。
  - 过程调用语句。
  - 返回语句。
- 分类：
  - 功能
    - 执行性：执行。
    - 说明性：声明。
  - 形式
    - 简单句
    - 复合句

文法

基本概念

文法：描述语法结构的形式规则。

字母表：是一个有穷字符集，记为Σ。

字符：字母表中的元素。

Σ上的字（字符串）：指由Σ中的字符构成的有穷序列。

空字：字符串中不包含任何字符的序列，记为ε。

Σ*：所有字的全体，包含空字。

Σ*的子集U，V的连接（积）定义为：

U V = {αβ | α∈U & β∈V} 也就是两个集合的所有字符串进行拼接得到的结果。

二者UV和VU运算结果不同，因为顺序不一样。

$V^n$：V的n次方。特别的，$V^0$ = { ε }。

V：是V的闭包，V = $V^0$ ∪ $V^1$ ∪ $V^2$ ∪ …

V+：V的正规闭包，V+ = V V*，正规闭包不会引入空字，其他一样。

->：定义，左边是被定义的对象，右边是定义内容。

上下文无关文法

设G是一个四元组：

G = (VT, VN, S, P) 其中： - VT：终结符集合，非空，是不能分解的单位 - VN：非终结符集合，非空，且 VT ∩ VN = ∅，是可以再分解的 - 不允许一个符号即是终结符，又是非终结符 - S：文法的开始符号，S∈VN - P：产生式的集合，每个产生式形式为： P -> α ，P ∈ VN，α∈(VT∪VN)*

例如定义：G = < {i, +, *, (, )}, {E}, E, P>，P由下列产生式组成：

E -> i
E -> E + E
E -> E * E
E -> (E)

巴科斯范式(BNF)：

定义符使用::=
表示文法：给出开始符号和产生式
文法化简：G(E): E -> i|E+E|E*E|(E)

推导
*

α1 $\Longrightarrow$ αn：经过0步或若干步推出
+
α1 $\Longrightarrow$ αn：经过1步或若干步推出

句型：S 星推出阿尔法是句型。

句子：仅含有终结符的句型是句子。

语言：文法G产生的句子的全体是语言。

L(G) = { α | S +推出阿尔法, α∈VT*}

例1：证明(i*i+i)是文法。由E开始推导。
例2：给出{a^n b^n | n>=1}的文法。

最左推导：替换最左边的终结符。
最右推导：替换最右边的终结符。
语法树：推导树。
二义性：

推导树不一样：二义文法；
可以由两个文法产生：二义语言。

无二义文法：
E -> T | E + T
T -> F | T * F
F -> (E) | i

形式语言（仅有产生式不一样，终结符，非终结符，文法开始符号都一样）：

0型文法：短语文法，图灵机。产生式：α -> β，α β ∈ (VT ∪ VN)*且至少包含一个非终结符。
1型文法：上下文有关文法，线性界限自动机。产生式：α -> β，α长度<=β长度，仅S->ε除外。
2型文法：上下文无关文法，非确定下推自动机。产生式：A -> β，A∈VN，β∈(VT ∪ VN)*，利用栈分析。
3型文法：正规文法，有限自动机。产生式：A -> αB或A -> α，α∈VT*，A B∈VN

词法分析

词法分析器

功能：输入源程序，输出单词符号
单词符号种类：
- 基本字，关键字
- 标识符：变量名，函数名等
- 常数
- 运算符
- 界符
输出
- 二元组（单词种别，单词自身的值）
- 种别：整数编码
- 值：标准二进制

词法分析器组成：

预处理：去除空白，跳格，回车、注释；区分符号区，句末符
输入缓冲区：接收文件
扫描器：驱动程序，输出单词符号
扫描缓冲区：接收预处理输出文本

扫描器：

起点指示器
搜索指示器
扫描缓冲区：分为两个半区，半区长度为单词最大长度。
超前搜索：使用限制减轻超前搜索任务
- 基本字
- 标识符
- 字符串
- 常数
- 其他

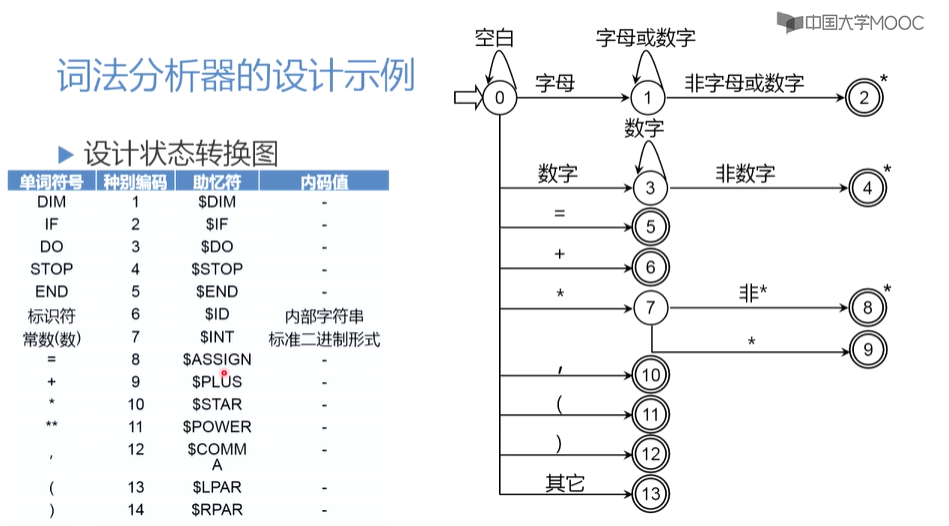
状态转换图

状态转换图：

结点：状态
状态之间用箭头表示，上面标记可能出现的输入字符和字符类
一张图只包含有限个状态，一个初态，至少一个终态。
可以用于识别和接收一定的字符串。
终态有两个圈套起来构成，加*表示退掉最后一个字符。
只有终态表示返回。

状态状态实现：

定义：
- ch：字符变量，存放最近一个读入字符
- strToken：字符数组
- GetChar：读入下一个字符ch
- GetBC：跳过空白符
- Concat：把ch连入strToken
- IsLetter，IsDisgital：判断是否为字母，数字
- Reserve：检查是否是保留字，并给出编码
- Retract：搜索指针退回一个位置
- InsertId：将标识符插入符号表，给出符号表指针
- InsertConst：将strToken插入常数表，返回常数表指针
实现：

int code, value;
char strToken[MAX_VALUE];

GetChar();
GetBC();
if(IsLetter()){  // 分支 1
  while(IsLetter() or IsDigit()){
    Concat();
    GetChar();
  }
  Retract();
  code = Reserve();
  if(code == 0){
    value = InsertId(strToken);
    return ($ID, value);
  }else{
    return (code, NULL);
  }
}else if(IsDigit()){  // 分支 2
  while(IsDigit()){
    Concat();
    GetChar();
  }
  Retract();
  value = InsertConst(strToken);
  return ($INT, value);
}else if(ch == '='){   // 分支 3 
  return ($ASSIGN, NULL);
}else if(ch == '+'){
  return ($PLUS, NULL);
}else if(ch == '*'){
  GetChar();
  if(ch == '*'){
    return ($POWER, NULL);
  }
  Retract();
  return ($STAR, NULL);
}else if(ch == ','){
  return ($COMMA, NULL);
}else if(ch == '('){
  return ($LPAR, NULL);
}else if(ch == ')'){
  return ($RPAR, NULL);
}else{
  ProcError();
}

状态图的代码化：

curState：现有状态
stateTrans[state][ch]：状态图，state当前状态，ch输入符号，返回下一个状态

curState = "初态"
GetChar();
while(stateTrans[curState][ch] is defined){
  Concat();
  curState = stateTrans[curState][ch];
  if (curState is FINAL_STATE){
    return strToken;
  }
  GetChar();
}

自动机

正规集，正规式

正规集：合法的单词和符号。

正规式：是表示正规集的方法。

正规式

ε和∅都是Σ上的正规式，表示的正规集为{ε}和∅
对于任意a∈Σ，a是Σ上的正规式，它表示的正规集为{a}
如果e1和e2都是Σ上的正规式，他们的正规集是L(e1)和L(e2)，则
- (e1|e2)为正规式，表示的正规集为L(e1)∪L(e2)，并集
- (e1·e2)为正规式，表示的正规集为L(e1)L(e2)，连接
- (e1)*为正规式，表示的正规集为( L(e1) )*，闭包

等价：如果两个正规式表示的正规集相同，则两个正规式等价。

例：证明：(a*b*)=(a|b)*

对于正规式满足：

或运算交换律
或运算结合律
或运算分配律
连接运算没有交换律

确定有限自动机 DFA

确定有限自动机 M = (S, Σ, f, S0, F)

S：有穷状态集
Σ：输入字母表（有穷）
f：状态转换函数 S x Σ -> S，例如f(s, a)=s’，表示当前状态s，输入字符a，转换为后继状态s’
S0：S0∈S，表示唯一的初态
F：F包含于S，表示终态的集合，可以为空，表示没有终态

设，M = ( {0, 1, 2, 3}, {a, b}, f, 0, {3} )

其中 f 定义为：
f(0, a)=1
f(0, b)=2
f(1, a)=3
f(1, b)=2
f(2, a)=1
f(2, b)=3
f(3, a)=3
f(3, b)=3

也可以写成矩阵形式：

	a	b
0	1	2
1	3	2
2	1	3
3	3	3

也可以画为状态转换图。

如果DFA M有m个状态，n个输入字符，则转换图有m个状态节点，每个节点最多有n个箭头射出，每个箭头用Σ上的不同输入字符来标记。

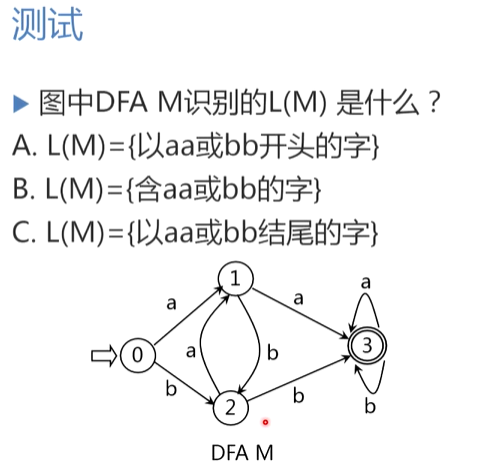
DFA M所识别的字的全体记为L(M)

DFA 的程序实现

curState = "初态"
GetChar();
while(stateTrans[curState][ch] is defined){
  Concat();
  curState = stateTrans[curState][ch];
  if (curState is FINAL_STATE){
    return strToken;
  }
  GetChar();
}

非确定有限自动机 NFA

非确定有限自动机 NFA，M = (S, Σ, f, S0, F)

S
Σ
f：S x Σ* -> 2^S 的部分映射，f(S, α)=S’，α是一个字，S’是一个状态的集合
S0：包含于S，是一个非空的初态集
F

特点：

可以有多个初态
弧上的标记可以是字，甚至是正规式
同一个字可以出现在多个同状态射出的弧上
DFA 是 NFA 的特例

NFA 转换为 DFA

如果两个有限自动机M和M’，如果L(M)=L(M’)，则二者等价。判定两个自动机等价的算法是存在的。

假设NFA M = (S, Σ, δ, S0, F)，改造过程如下

引入新增初态X和终态Y，X,Y∉S，
从X到S0中任意一个节点连接一条ε的弧
从F中任意节点连接一条到Y的ε弧。
对于 i —-AB—> j 子图，代换为 i –A–> k –B–> j
子集法

子集法

确定化

子集法

在状态表中，含有初态的集合视为初态，含有终态的集合视为终态。

DFA 化简

假设s和t为M的两个状态，满足如下调剂称为s和t为等价：

从s出发读到某个字α而终止于终态
从t出发也能读到α而终止于终态

把M的状态集划分为不相交的子集，使任何两个不同子集的状态是可区别的，同一子集的任何两个状态是等价的。最后，把每个子集选出一个代表，消去其他状态。

划分步骤：

划分S为终态和非终态
检查每个划分得到的子集是否能进一步划分
- 是否存在一个字符a，使得Ia不会包含在其他子集中

化简DFA

正规式与有限自动机

正规式与有限自动机可以等价。

为 NFA 构造正规式

假设NFA M = (S, Σ, δ, S0, F)，改造过程如下

加入X与Y，分别为新的初态和终态。
i –r1–> j –r2–> k 换为 i –r1r2–> k
i –r1–> j 和 i –r2–> j 换为 i –r1|r2–> k
i –r1–> j –r2–> j –r3–> k 换为 i –r1r2*r3–> k

为正规式构造 NFA

r1r2遍r1->j->r2
闭包，转换为指向自己的弧

语法分析

使用上下文无关文法。G=(VT,VN,S,P)

句子是仅含有终结符的句型。

分析方法：
自下而上：从输入串开始归约，LR分析，算符优先分析法
自上而下：从文法开始，寻找匹配，构造语法树，递归下降分析法

自上而下

从文法开始符号，推出句子。

出错时，就需要回溯。

在非终结符上要有候选，会产生回溯。

还会产生左递归问题。

消除左递归

左递归变右递归。

P->bP’
P’->aP’|e

间接左递归变右递归。

要求：不含回路，不含以e为右部的产生式

带入式子，消除多余非终结符。

再利用直接左递归方式。

消除回溯

FIRST集合。以指针指向的终结符开头。

制造FIRST，提取公共左因子。