计算机图形学

发表于 更新于 分类于 阅读次数：

…

基本介绍

渲染流水线：渲染管线，决定给定模式和纹理，生成二维图形。

应用程序阶段：产生顶点数据，摄像机位置，光照和纹理等。

几何阶段：变形投影后的定点，颜色，纹理。

光栅化：给每个像素正确配色。输出到屏幕的各个像素点颜色。

渲染管线

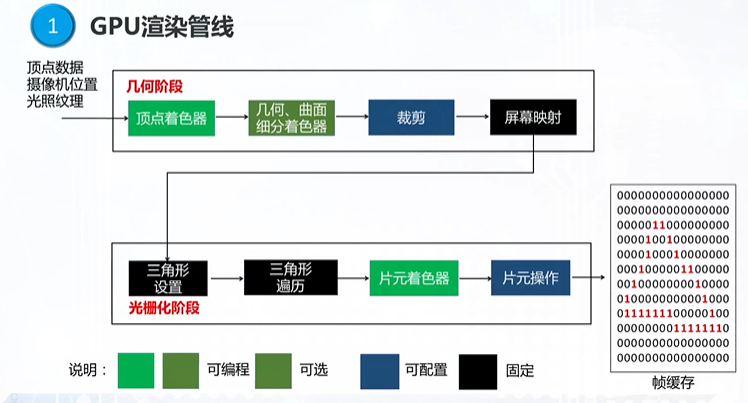
可编程：顶点着色器，几何/曲面细分着色器，片元着色器

可选：几何/曲面细分着色器

可配置：裁剪，片元操作

固定：屏幕映射，三角形设置，三角形遍历

顶点着色器：

  • 模型变换：将模型坐标映射到世界坐标
  • 视图变换：将世界坐标映射到摄像机中
  • 顶点着色

几何/曲面细分着色器：顶点增删，曲面细分

三角形遍历：求三角形覆盖的像素点，插值等方式

片元着色器：纹理贴图

着色器语言

Phong光照明模型，Cook着色树

Renderman，Pixiv公司

OpenGL GLSL，可以跨平台

GLSL

着色器：

  • 顶点着色器Vertex Shader
  • 几何着色器Geometry Shader
  • 曲面细分着色器Tessellation Shader
  • 片元着色器Fragment Shader

在OpenGL中使用着色器流程：

  • 创建着色器对象
  • 源码关联着色器对象
  • 编译着色器
  • 创建程序对象
  • 将着色器关联到程序对象

OpenGL通过uniform与GLSL通信。着色器之间通过in，inout，out调用函数。

数据类型：

  • 标量
  • 矢量，可以是2 3 4个分量
  • 矩阵
  • 结构和数组

控制结构，类似于C

EBO：索引缓冲区对象，存储顶点的索引信息

VBO：顶点缓冲区对象，存储顶点的各种信息，存入显存

VAO：顶点数组对象，对VBO组的引用

GLSL 实验

开发环境：

  • Visual Studio 2017
  • OpenGL3.3
  • GLSL330
  • GLFW
  • GLAD

工程目录：

  • src
    • .cpp
  • res
    • shader
    • texture
    • model
  • include
    • .h

过程：

初始化GLFW：

1
2
3
4
5
6
7
8
9
10
11
12
// 初始化GLFW
glfwInit();
// 配置主版本号
glfwWindowHint(GLFW_CONTEXT_VERSION_MAJOR, 3);
// 配置次版本号
glfwWindowHint(GLFW_CONTEXT_VERSION_MINOR, 3);
// 使用核心模式，无需向后兼容
glfwWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE);
// Mac OS X系统使用
glfwWindowHint(GLFW_OPENGL_FORWARD_COMPAT, GL_TRUE);
// 不可改变窗口大小，Mac OS
glfwWindowHint(GLFW_RESIZABLE, FALSE);

创建窗口：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int screen_width = 1280;
int screen_height = 720;

auto window = glfwCreateWindow(
    screen_width,   // 窗口尺寸
    screen_height,   
    "Window Title", // 标题
    nullptr,  // 是否全屏
    nullptr,  // 共享上下文（状态机）窗口
)

if(window == nullptr){
    return -1;
}
// 将窗口的上下文设置为当前线程的主上下文
glvwMakeContextCurrent(window);

初始化GLAD：

1
2
3
4
// 初始化GLAD，加载OPENGL函数指针地址的函数
if(!gladLoadGLLoader((GLADloadproc)glfwGetProcAddress)){
    return -1;
}

创建视口：

1
2
// 左下角位置，渲染窗口的宽，高
glViewport(0, 0, screen_width, screen_height);

数据处理：生成和绑定VBO，VAO，属性指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 三角形定点数据
const float triangle[] = {
    -0.5f, -0.5f,  0.0f, // 左下
     0.5f, -0.5f,  0.0f, // 右上
     0.0f,  0.5f,  0.0f  // 正上
}
// 生成与绑定VAO VBO
GLuint vertex_array_object; // VAO
glGenVertexArrays(1, &vertex_array_object);
glBindVertexArray(vertex_array_object);

GLuint vertex_buffer_object; // VBO
glGenBuffers(1, &vertex_buffer_object);
glBindBuffer(GL_ARRAY_BUFFER, vertex_buffer_object);

// 将定点数据绑定到缓冲，这样可以借助VBO将数据一次性发送过去
// GL_STATIC_DRAW表示图像不会变化
glBufferData(GL_ARRAY_BUFFER, sizeof(triangle), triangle, GL_STATIC_DRAW);

// 设置顶点属性指针
glVertexAttribPointer(
    0, // 顶点着色器位置
    3, // 顶点向量长度
    GL_FLOAT,  // 顶点类型
    GL_FALSE,  // 是否标准化
    3*sizeof(float),  // 步长
    (void*)0   // 数据在数组的偏移量
);
// 开启该通道
glEnableVertexAttribArray(0);

着色器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 顶点着色器
const char *vertex_shader_source = 
    "#version 330 core\n"
    "layout(location = 0) in vec3 aPos;\n"  // 位置变量的属性位置值 0
    "void main()\n"
    "{\n"
    "    gl_Position = vec4(aPos, 1.0);\n"
    "}\n\0";

// 片段着色器
const char *fragment_shader_source = 
    "#version 330 core\n"
    "out vec4 FragColor;\n"  // 输出的颜色向量
    "void main()\n"
    "{\n"
    "    FragColor = vec4(1.0f, 0.5f, 0.2f, 1.0f);\n"
    "}\n\0";

生成和编译着色器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 顶点着色器
int vertex_shader = glCreateShader(GL_VERTEX_SHADER);
glShaderSource(vertex_shader, 1, &vertex_shader_source, NULL);
glCompileShader(vertex_shader);

int success;
char info_log[512];
glGetShaderiv(vertex_shader, GL_COMPILE_STATUS, &success);
// 检查是否编译成功
if(!success){
    glGetShaderInfoLog(vertex_shader, 512, NULL, info_log);
    std::cout<<info_log<<std::endl;
    return -1;
}


// 片段着色器
int fragment_shader = glCreateShader(GL_FRAGMENT_SHADER);
glShaderSource(fragment_shader, 1, &fragment_shader_source, NULL);
glCompileShader(fragment_shader);

glGetShaderiv(fragment_shader, GL_COMPILE_STATUS, &success);
// 检查是否编译成功
if(!success){
    glGetShaderInfoLog(fragment_shader, 512, NULL, info_log);
    std::cout<<info_log<<std::endl;
    return -1;
}

链接着色器：

1
2
3
4
5
6
7
8
9
10
11
12
13
// 链接到着色器程序
int shader_program = glCreateProgram();
glAttachShader(shader_program, vertex_shader);
glAttachShader(shader_program, fragment_shader);
glLinkProgram(shader_program);
// 检查是否链接成功
glGetProgramiv(shader_program, GL_LINK_STATUS, &success);
if(!success){
    glGetProgramInfoLog(shader_program, 512, NULL, info_log);
    std::cout<<info_log<<std::endl;
    return -1;
}

删除着色器：

1
2
glDeleteShader(vertex_shader);
glDeleteShader(fragment_shader);

渲染：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
while(!glfwWindowShouldClose(window)){
    // 清空颜色缓存，使用黑色清空
    glClearColor(0.0f, 0.0f, 0.0f, 1.0f);
    glClear(GL_COLOR_BUFFER_BIT);
    // 使用着色器
    glUseProgram(shader_program);
    // 绘制三角形
    glBindVertexArray(vertex_array_object);  // 绑定VAO
    glDrawArrays(GL_TRIANGLES, 0, 3);        // 绘制三角形
    glBindVertexArray(0);                    // 解除绑定
    // 交换缓冲，双缓冲技术
    // 检查是否有触发事件，键盘，鼠标等
    glfwSwapBuffers(window);
    glfwPollEvents();
}

善后工作：

1
2
3
4
5
6
7
// 删除VAO VBO
glDeleteVertexArrays(1, &vertex_array_object);
glDeleteBuffers(1, &vertex_buffer_object);

// 清理资源，退出程序
glfwTerminate();
return 0;

扫描转换

软光栅：通过描述的点数据来光栅化对应的像素，通过软件实现。

光栅化方案：
点：直接四舍五入
直线：

  • 要求
  • 直线要直
  • 端点要准确，要无定向性和断裂
  • 亮度，色泽要均匀
  • 处理不同的线宽，颜色，线型
  • 算法
  • 驻点比较
  • 正负法
  • 数值微分
  • Bresenham算法
    圆：
  • 算法
  • 八分法
  • Bresenham算法
    多边形填充：
  • 算法
  • X 扫描线思想
  • Y 向连贯性算法
  • 边标志算法
    区域填充：
  • 表示
  • 边界表示法
  • 内点表示法
  • 分类
  • 4邻接点
  • 8邻接点
  • 算法
  • 种子填充算法
    • 4连通算法
    • 8连通算法
    • 边界填充（边界）
    • 泛填充（内点）
      属性：
  • 分类
  • 线型
  • 粗细
  • 颜色
  • 填充色（图案）
  • 算法
  • 线型：像素模板11101110
  • 线宽：像素模板
    • 线刷子（水平、垂直），线帽，折角处
    • 方刷子
  • 填充色：像素模板，遍历

数值微分

数值微分DDA，从直线的微分方程生成直线。
计算直线的微分方程，得到斜率 K。
根据K和起始点坐标，按照△x*t增量求下一个点。
t取值为1/max(|△x|, |△y|)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void DDAline(int x0, int y0, int x1, int y1)
{
    int dx, dy, espl, k;
    float x, y, xlncre, ylncre;
    dx = x1-x0;
    dy = y1-y0;
    if(abs(dx)>abs(dy)){
        espl = abs(dx);
    }else{
        espl = abs(dy);
    }
    xlncre = (float)dx/(float)espl;
    ylncre = (float)dy/(float)espl;
    for(k=0;k<=espl;k++){
        putpixel((int)(x+0.5), (int)(y+0.5));
        x += xlncre;
        y += ylncre;
    }
}

评价：算法容易实现，但是效率较低（浮点数）

Bresenham 直线算法

由直线的两个端点可以得到直线：F(x, y)=0

当 0<=k<=1 时：由当前点P0求得候选点为Pu(x(i+1), y(i+1))与Pd(x(x+1), y(i))。求这两个候选点的中点P(m, n)，如果中点处于直线上方，也就是F(m, n)>0，就选择Pd点；否则选Pu点。

构造判别式：d = F(x[i]+1, y[i]+0.5) = y[i]+0.5-k*(x[i]+1)-b
若d>=0，选Pd，否则选Pu。
即d>=0，y不变，否则增加1。

d 的递推计算：
d0 ：d = 0.5-k
d >= 0：d = d-k
d < 0：d = d-k+1

消除浮点数（放大为整数）：
d=d2
k=kdx

优化：
直接按照d选择Pu，Pd。
d = -0.5
d = d + k, x[i+1]=x[i]+1
d > 0.5：y[i+1]=y[i]+1, d=d-1
d <= 0.5：y[i+1]=y[i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void MidBrsenhamLine(int x0, int y0, int x1, int y1, int color)
{
    int dx, dy, d, UpIncre, DownIncre, x, y;
    if(x0 > x1){
        x=x1; x1=x0; x0=x;
        y=y1; y1=y0; y0=y;
    }
    x=x0; y=y0;
    dx=x1-x0;
    dy=y1-y0;
    d=dx-2*dy;
    UpIncre=2*dx-2*dy;
    DownIncre=-2*dy;
    while(x <= x1){
        putpixel(x, y, color);
        x++;
        if(d < 0){
            y++;
            d+=UpIncre;
        }else{
            d+=DownIncre;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void BrsenhamLine(int x0, int y0, int x1, int y1, int color)
{
    int dx, dy, e, x, y;

    dx=x1-x0;
    dy=y1-y0;
    e=-dx;
    x=x0;
    y=y0;
    while(x <= x1){
        putpixel(x, y, color);
        x++;
        if(e > 0){
            y++;
            e=e-2*dx;
        }
    }
}

八分法

将圆八等分，取其中一段圆弧，y=x与y轴正方向所夹圆弧，y=sqrt(R^2-x^2)
离散计算：
x[i+1]=x[i]+1, y[i+1]=sqrt(R^2-x[i+1])

先计算x还是先计算y，要看所选的圆弧在斜率是否大于1。

或使用极坐标，还是那一段圆弧：
a[i+1]=a[i]+da a -> 角度
x[i+1]=round(R*cos(a[i+1]))
y[i+1]=round(R*sin(a[i+1]))

Bresenham 圆算法

构造函数F(x, y)=x^2+y^2-R^2

将圆八等分，取其中一段圆弧，y=x与y轴正方向所夹圆弧。

此时最大位移方向是x方向，x每次加一，y不变或减1（两个候选点）。

计算d的递推和初值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void MidBrsenhamCircle(int r, int color)
{
    int d, x, y;

    x=0;
    y=r;
    d=1-r;
    while(x <= y){
        CirclePoint(x, y, color)
        if(d < 0){
            d+=2*x+3
        }else{
            y+=2*(x-y)+5;
            y--;
        }
        x++;
    }
}

Bresenham 椭圆算法

对于标准椭圆F(x, y)=b^2*x^2+a^2*y^2-a^2*b^2

将椭圆等分为4部分，同时判断x和y是否加1。

计算d的递推和初值。

X 扫描线

求得多边形各个顶点的y[min]与y[max]。

使用扫描线与多边形求交点。

对交点排序，填充交点之间的空间。

Y 向连贯性算法

构造多边形的边表：边表的长度是多边形的最大扫描线数，表上每个节点表示一个桶，桶上标明当前扫描线的y坐标。再将每条边放入该边y[min]的桶中。

每条新边记录的信息包括该边起点与x扫描线的交点x，该边的y[max]，斜率1/k（y+1时x的增量），下一条边指针next。

新边排序按照x坐标递增，如果交点相同则按增量递增。

对于每条边y[max]=y[max]-1，防止交点重复计算。

有效边表：当前扫描线与多边形相交的边构成的表。

扫描过程让有效边表与边表合并，并根据增量修改x值。通过顶点配对实现相应的填充。

边标志算法

对多边形的每个边进行直线扫描转换，给覆盖的点打上标记。

对扫描线上按照左闭右开的原则配对标记点并填色。

是适合硬件的算法。

种子填充算法

种子：区域内任意一点。

  1. 边界填充算法：
  • 输入：种子点坐标，填充色，边界色
  • 数据结构：栈
  • 算法输出：像素点集

4连通边界填充算法：种子入栈，执行下面步骤；
栈顶出栈，置为填充色，并检查4邻接点：如果不是边界色，且没有被填充则入栈。

  1. 泛填充算法：是内点且未被填充，则入栈。

  2. 扫描线填充：
    种子入栈；
    栈顶出栈，填充该行；
    检查扫描线上下的像素，其中最右边的入栈；

反走样技术

过取样（后滤波）：先提高取样分辨率，再取平均，降低分辨率。

对某一个像素扩充为3*3区域，并为区域上每一点赋予权值，再加权平均后合并为一个像素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void MidBrsenhamLine(int x0, int y0, int x1, int y1, int color)
{
    int dx, dy, d, UpIncre, DownIncre, x, y;
    int level;
    if(x0 > x1){
        x=x1; x1=x0; x0=x;
        y=y1; y1=y0; y0=y;
    }
    x=x0; y=y0;
    dx=x1-x0;
    dy=y1-y0;
    d=dx-2*dy;
    UpIncre=2*dx-2*dy;
    DownIncre=-2*dy;
    while(x <= x1){
        level = __level;  // 4个像素的亮度等级平均值
        putpixel(x, y, color);
        x++;
        if(d < 0){
            y++;
            d+=UpIncre;
        }else{
            d+=DownIncre;
        }
    }
}

前滤波：区域取样。对图形覆盖到的像素，根据图形与像素重叠部分占像素面积的比值计算像素点亮度；改进后可以使用圆形模板，通过在像素中心的距离上积分权值得到亮度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void AntialiasingLine(int x0, int y0, int x1, int y1, int I)
{
    int x, y, dx, dy, m, w, e;
    x=x0; y=y0;
    dx=x1-x0;
    dy=y1-y0;
    m=I*dy/dx;
    w=I-m;
    e=I/2;
    SetPixel(x, y, m/2);
    while(x < x1){
        if(e<w){
            x++; e+=m;
        }else{
            x++; y++; e-=m;
        }
        SetPixel(x, y, e);
    }
}

造型技术

图形对象

  • 非图形信息：线型，颜色，体积，重量等
  • 图形信息：点线面之间的关系，几何尺寸
  • 几何信息：位置大小
  • 拓扑信息：点边面等

图形的基本元素：体，面，环，边，顶点

顶点：0维度几何元素。

边：一维几何元素。可以是直线或曲线。

环：二维几何元素。外环一般为逆时针，内环一般为顺时针。

面：二维几何元素。必须有一个外环，可以没有内环。面有方向，用外法线表示。可以是平面或曲面。

体：三维几何元素。由封闭的表面围成。边界是有限面的并集。

几何造型：通过点线面体等几何元素经过平移，缩放，旋转和并，交，差等集合运算产生的物体模型。

实体

实体的性质：
刚性：必须有一定的形状。
维数一致性：一个物体的各部分是三维的。
占据优先空间：体积有限。
边界的确定性：能够区分出物体的内部和外部。
封闭性：经过任意计算后，仍然是有效物体。

实体的表面性质：
连通性：物体表面上任意两点可用实体表面上的一条路径连接。
有界性：物体表面可将空间分为互不连通的两部分，其中一部分是有界的。
非自相交性：物体表面不可自相交。
可定向性：表面的两侧可以明确定义出属于物体的内侧与外侧。
闭合性：由表面上的多边形网格各元素的拓扑关系决定。

克莱因瓶和莫比乌斯环则不符合上述性质。

正则形体：
三维空间中的正则集就是正则形体；
三维物体由内部点和边界点两部分， 内部点 构成的点集的 闭包 就是正则集。

二维流形：
对于实体表面上任意一点，在其任意小的领域内，该领域与平面上的圆盘是拓扑等价的。

实体：正则形体 + 二维流形

欧拉公式： V - E + F = 2（顶点 - 边 + 面 = 2）

欧拉公式适用于简单多面体（没有孔）。

对于非简单多面体：V - E + F - H = 2 * ( C - G )（顶点 - 边 + 面 - 孔 = 2 * （独立不相连多面体 - 贯穿孔））

样条

样条曲线：多项式曲线段连接的曲线。

样条曲面：由两组样条曲线描述。

插值样条曲线：选取适当的多项式让曲线经过每个控制点。

逼近样条曲线：选取多项式使部分或全部控制点不在生成的曲线上。

凸壳：包含一组控制点的凸多边形边界，是裁剪曲线的边界。

曲线控制图：由控制点连线构成的折线。

样条的描述方式：参数方程。

$$
x=x(u)
y=y(u)
z=z(u)
$$

在分段处还要给定连续性条件。
0阶参数连续性(C0连续性)：简单表示相连。
1阶参数连续性(C1连续性)：相连处一阶导数相等。
2阶参数连续性(C2连续性)：相连处一阶和二阶导数相等。

几何连续性：相怜处参数导数成正比。
0阶几何连续性(G0连续性)：简单表示相连。
1阶几何连续性(G1连续性)：相连处一阶导数成比例。
2阶几何连续性(G2连续性)：相连处一阶和二阶导数成比例。

样条表示：

  1. x(u) = ax*u^3 + bx*u^2 + cx*u^1 + dx, 0 <= u <= 1
  2. x(u) = [u^3 u^2 u^1 1] * [ax bx cx dx]^T = U * C
    C = Mspline * Mgemo
    Mgemo：四元素列矩阵，包含控制点的坐标和几何约束（边界条件）
    Mspline：4x4矩阵，几何约束值转化为多项式系数，提供样条曲线的特征。
  3. x(u) = g0 * BF0(u) + g1 * BF1(u) + ... + gk * BFk(u)
    gK：约束参数，控制点坐标和控制点曲线斜率。
    BFk(u)：混合函数，基本函数。

样条曲面：
P(u, v) = sum(P(ku,kv) * BF(ku)(u) * BF(kv)(v))

Bezier 曲线：
控制点，共n+1个，k从0到n：P[k] = (x[k], y[k], z[k])
函数路径：p(u) = sum(P[k] * BEZ[k,n] (u))
BEZ[k,n] (u)：Bernstein多项式：= C(n,k) * u^k * (1-u)^(n-k)
C(n,k)：二项式系数

Bezier 曲面：
由两组正交的Bezier曲线生成。
p(u,v) = sum_i( sum_j( P[i,j] * BEN[i,m] (u) * BEN[j,n] (v) ) )

模型表示

边界表示：用一组曲面描述物体

构造实体几何：使用基本实体运算得到

空间分割表示：描述物体的内部性质，由连续立方体堆叠成。

边界表示

多边形表面模型。

  • 数据结构：
  • 几何信息：
    • 顶点表
    • 边表
    • 面表，方向：右手法则
  • 拓扑信息：
    • 翼边结构
  • 属性信息：
    • 透明度
    • 材质
    • 纹理

多边形网络
曲面边界：三角形带，四边形网格。

扫描表示：
最终结果也是多边形表面模型。

构造实体表示

集合运算过程，可以用一个二叉树描述（CSG树）

  • 叶子：对象
  • 非叶子：操作
  • 根：CSG对象

通过光线投射算法，不必求解实体边界，可以快速实现光栅显示。

空间位置分割表示

使用三维数组P[I][J][K]表示物体空间占用情况。

使用八叉树表示实体，每个节点数据结构为：
01234567
BBBBBBBB
EBFBEBFE

E：Empty，空
F：Full，满
B：Boundary，边界

首先将整个空间分为8块，一个节点表示一个块。再将每个块细分为8个子块，每个子节点表示一个子块，如此细分下去，直到满足精度要求，如果是空或满则不必细分。

松散八叉树。

二叉空间分割，BSP树。每次将一个实体分为两半，方向任意。可以自适应分割，减少搜索时间。

BSP树：

  • 轴对齐分割：选取一个轴，将空间一分为二。
  • 多边形对齐分割。非常耗时。可以严格从前从后遍历。

BSP树可以用于碰撞检测。

分形

特点：

  • 不规则
  • 自相似

分形维数：把原图缩小为1/a的相似的b个图形，则有a^D=b。D 就是分形维数，可以是整数或分数。

生成过程：初试生成元，生成元。

例如：谢尔宾斯基三角形，科赫Koch雪花曲线。

形状语法：给定一组产生式规则，设计者可以根据规则获取物体。
例如：
L 语法：

  • 几何解释：
    • F 向前画线
    • 右转60°
    • 左转60°

粒子系统

用于模拟：水流，火，烟尘，爆炸，云雾，雪，流星，树叶等。

微粒系统：一组分散的微小物体集合，大小和形状可随时间变化。

模拟方式：

  • 随机过程模拟
  • 运动路径模拟
  • 力学模拟

两要素：

  • 造型
  • 运动方式

两过程：

  • 模拟
  • 渲染

粒子有生命值，要有产生和消亡过程。因此基本属性包括：位置，速度，颜色，大小，生命值。

公告板技术：粒子始终面向摄像机方向。

几何阶段

过程：

建模坐标系：局部空间
模型变换
世界坐标系：世界空间
视图变换
观察坐标系：观察空间
投影变换
观察坐标系：裁剪空间
屏幕映射
屏幕坐标系：屏幕空间

裁剪

保留观察空间内的物体。

物体与窗口关系：

  • 窗口内，保留。
  • 窗口外，舍弃。
  • 窗口上，计算交点判断。

基于编码的剪裁方式

Cohen-Sutherland方法：基于编码的剪裁方式。（二维平面，直线段）

  • 简取：两点都在窗口内部。
  • 简弃：两点都在窗口外部。如果两点都在上面（或下面，或左边，或右边）则弃。
  • 其他情况：将线段按交点分段，之后重复上述过程。

为每一个点赋予一个二进制编码D3 D2 D1 D0。

  • x < wxl：D0 = 1 否则 D0 = 0
  • x > wxr：D1 = 1 否则 D1 = 0
  • y < wyb：D2 = 1 否则 D2 = 0
  • y < wyt：D3 = 1 否则 D3 = 0

则wxl wxr wyb wyt所切割的平面被划分为9个区域，每个区域有一个独立的编码。

计算两个端点的编码code_1和code_2：

  • code_1|code_2 = 0：简取
  • code_1&code_2 != 0：简弃
  • 其他情况，求出交点再考虑。

中点剪裁法：在其他情况中，不再求交点，而是将线二等分再重复上述过程。

使用情况：大窗口，特小窗口。

Liang-Barsky 剪裁算法

首先对线段赋予方向，对任意直线段：IJ 有参数方程
x = x1 + u * (x2 - x1)
y = y1 + u * (y2 - y1)

如果在窗口内则有：
wxl <= x <= wxr
wyb <= y <= wyt

令p1 = x1 - x2 , q1 = x1 - wxl …
则u * pk <= qk , k = 1, 2, 3, 4 （左，右，下，上）

起点：Uone = max(0, u[k|pk < 0], u[k|pk < 0])
终点：Utwo = min(1, u[k|pk > 0], u[k|pk > 0])

最终得到直线的开始点和结束点，经过过滤不符合逻辑的线段，处理垂直和水平的线段后得到裁剪的线段。

多边形裁剪

Sutherland-Hodgeman 逐边裁剪算法，按窗口的左下右上的方法切割多边形，修改多边形的输出顶点。对于凹多边形有缺陷。

Weiler-Atherton 算法，按顺时针方向沿多边形边界追踪每一条边，记录每次穿过窗口的点。当从不可见进入可见区域，则输出可见线段。当从可见进入不可见区域，则沿窗口边界顺时针找到另外一个交点，输出两点间的线段。

Cohen-Sutherland 推广到三维：使用6位编码，分割空间为9个部分。

Liang-Barsky 推广到三维：之前是6个候选点，现在是8个候选点。

Sutherland-Hodgeman 推广到三维：裁剪三角形。

屏幕映射

由裁剪空间进入屏幕映射，坐标系由右手系变为左手系，这时z轴的方向反向。

z轴上的映射关系是：
裁剪空间：z=1 -> 屏幕空间：z'=0
裁剪空间：z=0 -> 屏幕空间：z'=0.5
裁剪空间：z=-1 -> 屏幕空间：z'=1

z' = (1-z)/2 + 0

这部分由GPU完成。

模型变换

在OpenGL中使用模型矩阵model实现。

1
2
3
4
glm::mat4 model(1);  // 创建模型
model = gml::translate(mode, glm::vec3(0.0f, 0.0f, -3.0f));  // 平移
model = gml::rotate(mode, (float)glfGetTime(), glm::vec3(0.0f, 1.0f, 0.0f));  // 旋转
model = gml::scale(mode, glm::vec3(0.5f, 0.5f, 0.5f));  // 缩放

视图变换

在OpenGL使用视图矩阵实现。

1
2
3
glm::mat4 view(1);
// 摄像机的位置，目标位置Zv，上方向量Yv，坐标系符合右手定则
view = glm::lookAt(camera_pos, camera_pos + camera_font, camera_up);

投影变换

在OpenGL使用视图矩阵projection实现。

1
2
3
4
5
6
glm::mat4 proj = glm::perspective(
    45.0f,   // 视野的角度 fov
    (float)width/(float)height,  // 视窗的宽高比
    0.1f,    // 前截面
    100.0f   // 后截面
);

PVM 矩阵

将Model，View，Projection合并为PVM矩阵。

1
gl_Pos = projection * view * model * vec4(aPos, 1.0f);  // 顺序不能出错，计算从右向左

在OpenGL中，向量都是列矩阵，而之前的理论推导均为行矩阵，因此需要倒过来计算。

旋转立方体

模型设置：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 创建模型
glm::mat4 model(1); // 局部坐标转换到世界坐标
// 平移旋转模型
model = glm::translate(model, glm::vec3(0.0f, 0.0f, 0.0f));
model = glm::rotate(
    model, 
    (float)glfwGetTime(),  // 以当前时间作为旋转角度
    glm::vec3(0.5f, 1.0f, 0.0f)  // 旋转轴
);
// 观察矩阵
glm::mat4 view(1);
view = glm::lookAt(camera_pos, camera_pos + camera_font, camera_up);
// 投影矩阵
glm::mat4 projection = glm::perspective(
    glm::radians(fov),   // 视野的角度 fov
    (float)screen_width/(float)screen_height,  // 视窗的宽高比
    0.1f,    // 前截面
    100.0f   // 后截面
);


摄像机控制：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 键盘事件
void ProcessInput(GLFWwindow *window)
{
    // ESC 关闭窗口
    if(glfwGetKey(window, GLFW_KEY_ESCAPE) == GLFW_PRESS){
        if(glfwSetWindowShouldClose(window, true));
    }

    // 按 W 向前移动
    float camera_speed = 2.5f * delta_time;
    if(glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS){
        camera_pos += camera_speed * camera_front;
    }
}

// 注册鼠标相应
glfwSetCursorPosCallback(window, MouseCallback);

// 鼠标事件
void MouseCallback(GLFWwindow *window, double xpos, double ypos)
{
    glm::vec3 front;
    front.x = cos(glm::radians(yaw) * cos(glm::radians(pitch)));
    front.y = sin(glm::radians(pitch));
    front.z = sin(glm::radians(yaw) * cos(glm::radians(pitch)));
    camera_front = glm::normalize(front);
}

将PVM传入着色器：

1
2
3
4
// 获取着色器内某个参数的位置
int model_location = glGetUniformLocation(our_shader.ID, "model");
// 写入参数值
glUniformMatrix4fv(model_location, 1, GL_FALSE, glm::value_ptr(model));

开启深度测试：

1
2
3
glEnable(GL_DEPTH_TEST); // 开启深度测试
glDepthFunc(GL_LESS);    // 深度测试，输入的深度小于参考值则通过

几何变换

二维变换

例如在二维空间下：

平移变换：
x' = x + Tx
y' = y + Ty

比例变换：
x' = x * Sx
y' = y * Sy

旋转变换：
x' = r * cos(A + B)
y' = r * sin(A + B)

x' = x * cosA - y * sinA
y' = x * sinA + y * cosA

对称变换：5种情况
x' = x
y' = -y

错切变换：
x' = x + d * y
y' = b * x + y

使用齐次坐标表达方式，可以用3维向量表示2维向量，来简化计算。例如：p[x, y] 表示为 p[hx, hy, h]，h为不为0的系数，规范化表示：令h = 1。

这样，就可以使用齐次坐标与变换矩阵相乘得到结果。

对于变换矩阵
左上部分(4)：图像的比例，旋转，对称，错切
右上部分(2)：投影
左下部分(2)：平移
右下部分(1)：整体的比例变换

平移变换：
$$
\left[
\begin{matrix}
1 & 0 & 0 \
0 & 1 & 0 \
Tx & Ty & 1
\end{matrix}
\right] \tag{1}
$$

比例变换：
$$
\left[
\begin{matrix}
Sx & 0 & 0 \
0 & Sy & 0 \
0 & 0 & 1
\end{matrix}
\right] \tag{2}
$$

旋转变换：
$$
\left[
\begin{matrix}
cosA & sinA & 0 \
-sinA & cosA & 0 \
0 & 0 & 1
\end{matrix}
\right] \tag{3}
$$

对称变换：5种情况
$$
\left[
\begin{matrix}
1 & 0 & 0 \
0 & -1 & 0 \
0 & 0 & 1
\end{matrix}
\right] \tag{4}
$$

错切变换：
$$
\left[
\begin{matrix}
1 & b & 0 \
c & 1 & 0 \
0 & 0 & 1
\end{matrix}
\right] \tag{5}
$$

运算完毕后，对齐次坐标进行规范化（最后一项h）。

三维变换

在3维空间中的齐次坐标表示为p[hx, hy, hz, h]，变换矩阵含义依然不变。

平移变换：
$$
\left[
\begin{matrix}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & 0 \
Tx & Ty & Tz & 1
\end{matrix}
\right] \tag{6}
$$

比例变换：
$$
\left[
\begin{matrix}
Sx & 0 & 0 & 0 \
0 & Sy & 0 & 0 \
0 & 0 & Sz & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{7}
$$

旋转变换（右手定则）：

绕z轴转动：
$$
\left[
\begin{matrix}
cosA & sinA & 0 & 0 \
-sinA & cosA & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{8}
$$

绕x轴转动：
$$
\left[
\begin{matrix}
1 & 0 & 0 & 0 \
0 & cosA & sinA & 0 \
0 & -sinA & cosA & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{9}
$$

绕y轴转动：
$$
\left[
\begin{matrix}
cosA & 0 & -sinA & 0 \
0 & 1 & 0 & 0 \
sinA & 0 & cosA & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{10}
$$

对称变换：
$$
\left[
\begin{matrix}
1 & 0 & 0 & 0 \
0 & -1 & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{11}
$$

错切变换：
$$
\left[
\begin{matrix}
1 & b & c & 0 \
d & 1 & f & 0 \
g & h & 1 & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{12}
$$

也就是x' = x + d*y + g*z

三维逆变换

平移变换：
$$
\left[
\begin{matrix}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & 0 \
-Tx & -Ty & -Tz & 1
\end{matrix}
\right] \tag{6}
$$

比例变换：
$$
\left[
\begin{matrix}
1/Sx & 0 & 0 & 0 \
0 & 1/Sy & 0 & 0 \
0 & 0 & 1/Sz & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{7}
$$

旋转变换（右手定则）（带入 -A）：

绕z轴转动：
$$
\left[
\begin{matrix}
cosA & -sinA & 0 & 0 \
-inA & cosA & 0 & 0 \
0 & 0 & 1 & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{8}
$$

绕x轴转动：
$$
\left[
\begin{matrix}
1 & 0 & 0 & 0 \
0 & cosA & -sinA & 0 \
0 & sinA & cosA & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{9}
$$

绕y轴转动：
$$
\left[
\begin{matrix}
cosA & 0 & sinA & 0 \
0 & 1 & 0 & 0 \
-sinA & 0 & cosA & 0 \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{10}
$$

三维复合变换

分析步骤：

  1. 先将参考点移动到坐标原点（轴）
  2. 进行相应变换
  3. 在移动到原来位置

观察变换

设观察参考点P0[Xv, Yv, Zv]，观察坐标系为右手定则。

观察变换：将世界坐标系中的点Q变换到观察坐标系中。

分析步骤：

  1. 平移观察参考点到用户坐标系原点
  2. 进行旋转变换，将三个坐标轴重合
  3. 此时新得到的Q就是所求了

投影变换

在观察变换中隐含了一个观察平面，也就是投影平面。

平行投影：三视图

  • 正投影
  • 三视图：常用反应尺寸，但难以表达三维性质
  • 正轴测图：垂直投影方向
  • 等轴测，正二测，正三测
  • 斜投影：投影方向不垂直与投影面
  • 斜等测，斜二测

透视投影：近大远小
一点透视：1个主灭点，投影面与1个坐标轴正交，与另外2个轴平行
两点透视：2个主灭点，投影面与2个坐标轴正交，与另外1个轴平行
三点透视：3个主灭点，与3个坐标轴都相交

在变换矩阵的右上角，是有关投影的设置。
一点透视：相似成比例
x’ = x / (z/d)
y’ = y / (z/d)
z’ = d

变换矩阵：
$$
\left[
\begin{matrix}
1 & 0 & 0 & 0 \
0 & 1 & 0 & 0 \
0 & 0 & 1 & 1/d \
0 & 0 & 0 & 1
\end{matrix}
\right] \tag{10}
$$

观察空间

根据观察平面可以定义观察空间，根据投影方式不同，会产生出不同的形状观察空间。根据前截面和后截面的定义，还能得到观察空间的范围。

得到的有限观察空间又叫裁剪空间，视景体。

这里可以定义规范化的投影空间：
观察窗口在XoY面上x = ±1, y = ±1，前截面和后截面为z = ±1
正投影：经过比例、平移变换得到投影空间。
斜平行投影：经过比例、平移、错切变换得到投影空间。
透视：透视变换。

这部分可以直接使用函数调用：

1
glm::mat4 proj = glm::perspective(45.0f, 1.3f, 0.1f, 100.0f);

之后就是裁剪和屏幕映射了。

光栅化阶段

首先是收集三角形，之后遍历三角形覆盖的像素，并对像素着色。最后通过片元操作（遮挡，透明等）得到三角形的真实像素。

视觉现象

颜色辨别

  • 对青绿色和橙黄色最敏感
    颜色对比：由视觉暂留效应引起
  • 同时对比：环境色影响某一颜色的判断
  • 即时对比：观察浅绿色后，再看黄色，会感觉到猩红
  • 边界对比：多种颜色的边界处对比强烈（马赫带效应）
  • 色相对比：同类色(15)，邻近色(45)，对比色(90-120)，互补色(180)
  • 明度对比：颜色受环境的明度影响
  • 纯度对比：环境纯度低会使物体显得鲜亮
    颜色错觉：
  • 同化现象：纹理会使背景色偏亮(暗)，纹理越接近背景，同化越明显
  • 色彩的醒目性
  • 色彩的进退：色块有前有后，对比度大时有进的感觉，反之有退的感觉
  • 色彩的冷暖
  • 色彩的胀缩
  • 色彩的软硬
  • 色彩的情绪

颜色的表示

颜色的三特性：明度，色调，饱和度。
组合成空间表示–纺锤体：上下两个极端为明度中的白和黑；中间一圈表示色调；由圆心向外辐射表示饱和度。

CIE色度图：舌型曲线。

RGB, CMY：面向设备

HSV, HSL：面向用户，六棱锥形状，纺锤体状

OpenGL中的颜色模型：
存储方式：

  • 颜色索引
  • 颜色值
    • RGB 颜色模式，每个分量取值0~1
    • RGBA 颜色模式，多一个不透明度，1表示不透明
      • 颜色混合：源颜色值s，源调和因子S，目标颜色值d，目标调和因子D
        • 调和颜色：SrRs + DrRd, SgGs + DgGd, SbBs + DbBd, SaAs + DaAd
    • HDR：高动态范围图像，为了保留大于1.0的颜色值的细节，将颜色重新归一化

光照模型

基本概念

环境光：弥漫于整个空间的光线。不是来自于光源，而是来自于无限多的反射得到。

  • 特点：照射到物体表面的光均匀的来自于各个方向，并均匀的向各个方向反射。
  • 表示：Ie = Ia * Ka
    • Ia：环境光强度
    • Ka：物体对环境光的反射系数

漫反射光：设点光源发出光强为Ip的光，向四周均匀辐射。物体得到的漫反射光取决于与光源的距离和朝向。

  • 理想漫反射：在一个粗糙，无光泽的表面上，光线沿各个方向做相同的反射，亮度相同。
  • 特点：光源唯一，反射光均匀反射。
  • 表示：Id = Ip * Kd * cosA
    • Ip：点光源亮度
    • A: 入射光与法线夹角
    • Kd：漫反射系数，与物体材料和光的波长决定

镜面反射：遵循反射定理，强度很大。

  • 理想反射：观察者和点光源在物体表面有，入射角等于反射角
  • 非理想反射：入射角不等于反射角，但是依然可以看到高光
  • 表示：Is = Ip * Ks * (cosA)^n
    • Ks：镜面反射系数
    • A：反射镜与观察者夹角的差值
    • n：反射指数，数目越大，物体越光滑，高光光斑越聚焦
    • 公式为经验公式

综合表示：I = Ia * Ka + Ip * Kd * (L · N) + Ip * Ks * (R · V)^n

Phong 模型

为了简化计算，做近似处理

近似处理：I = Ia * Ka + Ip * Kd * (L · N) + Ip * Ks * (H · N)^n

  • 假设光源和视点在无穷远，采用平行投影，则L与V变为常量
  • 取H为(L+V)/2，N为法线
  • 最终得到高光的方向为一个常量。
  • 误差：高光区域变大，通过适当调高n修正。

光强衰减：距离为d时

  • 最简单的衰减因子：1/(d^2)
  • 实际使用：f(d) = min(1, 1/(c0 + c1 * d + c2 * d^2))

此时的光强：I = Ia * Ka + f(d) * Ip * Kd * (L · N) + f(d) * Ip * Ks * (H · N)^n

此外，对RGB三个通道需要分别计算光强，需要的参数包括三种颜色的反射系数，三种颜色的光强。

消除马赫带效应的方法：

  • 多边形细分
  • 光照插值
  • 明暗处理：对顶点法向量做双线性插值

平行光：不加衰减因子
点光源：保留衰减因子
聚光灯：光锥的内圆锥和外圆锥，中间是渐变

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// 平行光
vec3 CalcDirLight(DirLight light, vec3 normal, vec3 viewDir)
{
    if(!light.on){
        return vec3(0.0f);
    }
    // 漫反射
    vec3 lightDir = normalize(-light.direction);
    float diff = max(dot(normal, lightDir), 0.0f);
    // 镜面反射
    vec3 reflectDir = reflect(-lightDir, normal);
    float spec = pow(max(dot(viewDir, reflectDir), 0.0f), material.shininess);
    // 漫反射 物体颜色
    vec3 diffuseColor = vec3(material.diffuse);
    // 叠加颜色
    vec3 ambient = light.ambient * diffuseColor;
    vec3 diffuse = light.diffuse * diff * diffuseColor;
    vec3 specular = light.specular * spec * vec3(material.specular);

    return ambient + diffuse + specular;
}
// 点光源
{
    ...
    float d = lenght(light.postion - fragPos);
    float attenuation = 1.0 / (light.c + light.l * d + light.q * d * d);
    ...
    return (ambient + diffuse + specular) * attenuation;
}
// 聚光灯
{
    ...
    float theta = dot(lightDir, normalize(-light.direction));
    float epsilon = light.cutOff - light.outerCutOff;
    float intensity = clamp((theta - light.outerCurOff)/ epsilon, 0.0f, 1.0f);  // clamp 约束强度在 0 到 1 之间
    ...
    return (ambient + (diffuse + specular * intensity)) * attenuation;
}

Whitted 光透射模型

全局光照(GI)，又叫间接光照。

间接光照：

  • 来源：其他物体的反射，透射的折射光。

在原来的基础上加入透射光强和反射光源。

透射光强：It * Kt

  • Kt：透射系数

反射光源：Ir * Kr

  • Kr：反射系数（镜面反射）

综合表示：I = Ia * Ka + Ip * Kd * (L · N) + Ip * Ks * (R · V)^n + It * Kt + Ir * Kr

全局光照的主要算法：

Ray Tracing：光线追踪
Path Tracing：路径追踪
Photon Mapping：光子映射
Point-based Global Illumilation：基于点的全局光照
Voxel-based Global Illumilation：基于体素的全局光照
Ambient Occlusion：环境光遮蔽

光线追踪

光线投射：从观察平面的每个像素射出一条射线，找到最接近的物体挡住射线的路径，得到光强。

光线追踪：在光线投射的前提下，加入物体表面的反射，折射，直到与光源相交。

计算方法：如果是漫反射，则直接计算该点被光源照射的颜色；如果是镜面反射或折射，则继续反射或折射到另一条光线。如此递归，直到达到结束条件（遇到光源，逃逸出场景，达到最大深度。

缺陷：

  • 表面属性单一：完全没有折射光或反射光。
  • 不考虑漫反射：漫反射成为结束条件。

修正：

  • 把表面属性改为混合的（反射20% + 折射30% + 漫反射50%）
  • 使用蒙特卡洛近似简化。

路径追踪：光线追踪 + 蒙特卡洛方法

纹理

纹理类型：

  • 颜色纹理：花纹，图案
  • 几何纹理：表面微观几何形状

颜色纹理

纹理模式：

  • 图像纹理
  • 函数纹理：使用函数定义简单的二维纹理，或随机高度场，或粗糙的几何纹理。

纹理映射：
首先定义纹理模式，建立物体表面的点与纹理模式点之间的对应。
其次对应点与光照模型进行计算。

纹理空间：二维单位正方形区域，描述纹理。

纹理映射方法：

  • 建立物体空间表面和纹理空间的对应关系
    • 对物体表面坐标(x, y, z)用u, v参数化
    • 反求参数u, v用(x, y, z)表达
    • 根据u, v得到纹理值，并带入光照模型

纹理映射代码：

1
2
3
4
5
6
7
8
9
// 设置纹理属性
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
// 加载纹理
unsigned char *data = stbi_load("res/texture/contain.jpg", &width, &height, &nrchannels, 0);
// 生成纹理
glGenTexutres(1, &texture1);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height 0, GL_RGB, GL_UNSIGNED_BYTE, data);
// 绑定纹理
glBindTexture(GL_TEXTURE_2D, texture1);

立方体贴图：

  • 盒子贴图
  • 天空盒贴图

纹理贴图过程

纹理的定义和设置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 创建纹理
GLuint texture1;
glGenTextrues(1, &texture1);
glBindTexture(GL_TEXTURE_2D, texture1);
// S轴(x轴)方向上环绕方式 
// GL_REPEAT：重复
// GL_MIRRORED_REPEAT：重复且镜像
// GL_CLAMP_TO_EDGE：超出部分拉伸
// GL_CLAMP_TO_BORDER：超出部分填入其他颜色
glTextParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
// T轴(y轴)方向上环绕方式
glTextParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
// 纹理缩小的时候，过滤方式是 线性过滤：产生颗粒状图案，能更清晰看到纹理像素
glTextParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
// 纹理放大的时候，过滤方式是 临近过滤：产生平滑图案
glTextParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

载入资源

1
2
3
4
5
6
7
8
int width, height, nrchannels;
stbi_set_flip_vertically_on_load(true);
unsigned char *data = stbi_load("a.jpg", &width, &height, &nrchannels, 0);
if(data){
  // 生成纹理
}else{
  // 载入失败
}

生成纹理

1
2
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, width, height, 0, GL_RRGB, GL_UNSIGNED_BYTE, data);
glGenerateMipmap(GL_TEXTURE_2D);

绑定纹理

1
2
3
4
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, texture1);
...
glDrawArrays(GL_TRANGLES, 0, 36);  // 绘制

立方体数据

1
2
3
4
5
const float vectices[] = {
  -0.5f, -0.5f, -0.5f,  0.0f,  0.0f, // 后面的两个是纹理的U V参数
  ...
}
// 如果使用立方体贴图，则不需要U V 参数

着色器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// box.vs 顶点着色器
#version 330 core
layout(location = 0)
in vec3 aPos;
layout(location = 1)
in vec2 aTexCoord;
out vec2 TexCoord;
...
void main(){
  gl_Position = projection * view * model * vec4(aPos, 1.0);
  TexCoord = vec2(aTexCoord.x, aTexCoord.y);
}

// box.fs 片元着色器
#version 330
coreout vec4 FragColor;
in vec2 TexCoord;
uniform sampler2D texture1;
void main(){
  FragColor = texture(texture1, TexCoord);
}

// skybox.vs
#version 330 core
layout(location = 0)
in vec3 TexCoords;
uniform mat4 projection;
uniform mat4 view;
void main(){
  TexCoord = aPos;
  vec4 pos = projection * view  * vec4(aPos, 1.0);
  gl_Position = pos.xyww; // z变为w，让其永远在最后面当背景
}

// skybox.fs
#version 330
out vec4 FragColor;
in vec3 TexCoords;
uniform samplerCube skybox;
void main(){
  FragColor = texture(skybox, TexCoords);
}

天空贴图可以使用立方体贴图：

 Top

Left Front Right Back
Bottom

立方体贴图有自己特殊的属性，可以使用方向向量对其索引和采样。

纹理定义：

1
2
3
4
5
6
7
8
9
10
11
12
unsigned int load_cubemap(std::vector<std::string> faces){
  unsigned int textureID;
  glGenTextrues(1, &textureID);
  glBindTexture(GL_TEXTURE_CUBE_MAP, textureID);
  ...
  glTextParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
  glTextParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
  glTextParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);
  glTextParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
  glTextParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
  return textureID;
}

资源载入：

1
2
3
4
5
6
7
8
unsigned int load_cubemap(std::vector<std::string> faces){
  int width, height, nrchannels;
  for(unsigned int i = 0; i < 6; i++){
    glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_RGB, width, height, 0, GL_RGB, GL_UNSIGNED_BYTE, data);
  }
  ...
  return textureID;
}

天空盒不需要世界坐标系的模型变换，又由于相机始终在天空盒中心点，因此要消去view矩阵的位移部分。

1
view = glm::mat4(glm::mat3(glm::lookAt(camera_position, camera_position + camera_front, camera_up)));  // 去除相机位移

几何纹理

对物体表面的几何性质做微小扰动，产生凹凸不平的细节效果。
例如物体表面P(u, v)，都沿着法向量方向位移F(u, v)个单位长度，新表面的位置：P'(u, v) = P(u, v) + F(u, v) * N(u, v)，最终还是利用光照产生立体感。

算法：

  • Bump Mapping 凹凸贴图：计算顶点光强时，给原始法向量加入一个扰动。
  • Displacement Mapping 移位贴图：直接作用于顶点，根据像素值，使顶点沿发现移动，产生真正的凹凸平面。
  • Normal Mapping 法线贴图：通过height map获得法向量信息，用RGB表示法向量的XYZ，之后计算光强，产生凹凸阴影效果。
  • Parallax Mapping 视差贴图：通过height map和视线，陡峭的视角给顶点更多的位移，否则给少量位移，通过视差获得立体感。
  • Relief Mapping 浮雕贴图：更精确的找出观察者视线与高度的交点，实现精确位移。

法线贴图：
height map，高度图：

  • 存储的RGB值，实际上是法线的XYZ。
  • 光照后颜色值发生变换产生凹凸不平的效果。
  • 一个平面上的定点法向量方向根据height map取值。
  • height map的法向量需要根据平面调整到全局情况中。

切线空间的引入：

  • 每个平面有一个自己的切线空间
    • T：tangent 切线，x轴
    • B：bitangent 副切线，y轴
    • N：normal 法线，z轴
  • 通过平面上不共线3点确定TBN的方向量(TBN矩阵)
  • TBN矩阵叠加到法向量方向上得到法线贴图

法线贴图使用

一般height map偏蓝色，因为蓝色B表示z轴方向，指向用户。

使用height map：

1
2
3
4
GLuint cube_diffuse_texture = LoadTextureFromFile(".jpg"); // 纹理
GLuint cube_normal_texture = LoadTextureFromFile(".jpg");  // 法线

Shader normalmap_shader(".vs", ".fs");  // 加载着色器

在着色器中使用法线贴图：

1
2
3
4
5
6
7
8
9
10
11
...
uniform sampler2D texture_material;
uniform sampler2D texture_normal;
...
void main(){
  vec3 normal = texture(texture_normal, fs_in.TexCoords).rgb; // 采样
  normal = normalize(normal * 2.0 - 1.0);  // RGB(0,1)范围转换到法线(-1,1)
  ...
  vec3 result = ambient + diffuse + specular;
  FragColor = vec4(result, 1.0);
}

引入切线空间：

1
2
3
4
5
6
7
8
9
10
11
12
// 获取TBN矩阵
layout (location = 1) in vec3 aNormal;
layout (location = 3) in vec3 aTangent;
// 计算TBN矩阵，右手系
vec3 T = normalize(vec3(model * vec4(aTangent, 0.0f)));
vec3 N = normalize(vec3(model * vec4(aNormal, 0.0f)));
vec3 B = normalize(cross(T, N));
vs_out.TBN = mat3(T, B, N);  // 传出TBN矩阵
// 引入切线到世界空间变换
normal = texture(normalMap, fs_in.TexCoords).rgb;
normal = normalize(normal * 2.0 - 1.0);
normal = normalize(fs_in.TBN * normal);

着色器：

1
2
3
4
5
6
7
8
9
10
11
12
...
uniform sampler2D texture_material;
uniform sampler2D texture_normal;
...
void main(){
  vec3 normal = texture(texture_normal, fs_in.TexCoords).rgb; // 采样
  normal = normalize(normal * 2.0 - 1.0);  // RGB(0,1)范围转换到法线(-1,1)
  // 引入切线到世界坐标变换
  normal = normalize(fs_in.TBN * normal);
  // 处理光照
  ...
}

阴影

基本思想：将视点移动到光源位置，用多边形区域排序消隐算法将多边形分为两类：向光与背光。再将视点移动到原来位置，对向光和背光多边形进行消隐，选用一种光照模型计算多边形亮度。

例如使用Phong模型，则对背光多边形只保留环境光。

主流算法：
Shadow Mapping：物体处于阴影是因为它与光源之间存在遮蔽物。
Shadow Volumn：根据光源和遮蔽物位置关系计算场景的阴影区域，然后对所有物体检测，确定是否受阴影影响。

Shadow Mapping

步骤：

  1. 以光源为视点，对场景进行渲染，得到一幅所有物体相对于光源的depth map(shadow map)，每个位置存储该点上离最近片元的深度值。
  2. 恢复视点位置，对每个像素计算和光源的距离，将该值与depth map的值比较，确定该像素是否存在阴影当中。根据是否处于阴影，使用不同的光照计算策略。

存在问题：阴影失真
解决方法：使用阴影偏移，简单对表面加入偏移量，让片元在表面上方。

使用FBO存储Shadow Map：
一个完整的帧缓冲(FBO)需要：

  • 至少一个缓冲：颜色，深度，模板缓冲
  • 至少一个颜色附件：Attachment
  • 所有附件是完整的：保留了内存
  • 每个缓冲都有相同的样本数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 创建并绑定一个帧缓冲
unsigned int fbo;
glGenFramebuffers(1, &fbo);
glBindFramebuffer(GL_FRAMEBUFFER, fbo);
// 绑定附件 使用纹理存储shadow map
unsigned int texture;
glGenTextures(1, &texture);
glBindTexture(GL_TEXTURE_2D, texture);
glTexImage2D(GL_TEXTURE_2D, 0, GL_RGB, 800, 600, 0, GL_RGB, GL_UNSIGNED_BYTE, NULL);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
// 附加到帧缓冲上
glFramebufferTexture2D(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_TEXTURE_2D, texture, 0);
// 检查帧缓冲完整性
if (glCheckFramebufferStatus(GL_FRAMEBUFFER) == GL_FRAMEBUFFER_COMPLETE){
  // 帧缓冲完整
}
// 处理后续工作
glBindFramebuffer(GL_FRAMEBUFFER, 0);
glDeleteFramebuffers(1, &fbo);

产生阴影效果：

1
2
3
4
5
6
7
8
9
10
// 渲染阴影深度贴图
glBindFramebuffer(GL_FRAMEBUFFER, dpethMapFBO);
glClearColor(0.1f, 0.1f, 0.1f, 0.1f);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glViewport(0, 0, SHADOW_WIDTH, SHADOW_HEIGHT);
// 传入着色器
shaodwMap_shader.use()
shadowMap_shader.setMat4("lightSpaceMatrix", lightSpaceMatrix);
renderScene(shadowMap_shader);
glBindFramebuffer(GL_FRAMEBUFFER, 0);

利用帧缓冲中的shadow map，判断是否是阴影部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 判断阴影
float ShadowCalculation(vec4 flagPosLightSpace)
{
  vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
  // 变换范围到 0 1 之间
  projCoords = projCoords * 0.5 + 0.5;
  float closestDepth = texture(shadowMap, porjCoores.xy).r;
  float currentDepth = projCoords.z;
  float shadow = currentDepth > closestDepth ? 1.0 : 0.0;
  return shadow;
}
// 渲染阴影
float shadow = ShadowCalculation(fs_in.FragPosLightSpace);
vec3 lighting = (ambient + (1.0 - shadow) * (diffuse + specular)) * color;

问题：实际会遇到采样越界，阴影失真，锯齿感等问题。

片元操作

片元操作包括

  • 模板测试：遮罩效果
  • 深度测试：透明，半透明，不透明效果
  • 颜色混合：运动模糊，泛光效果等
  • 最终输出到颜色缓冲区

颜色缓存：存储每个像素点颜色值

深度缓存：存储每个像素点的深度值

模板缓存：存储模板，用于显示输出区域，例如规定值为1的点会被显示

累计缓存：存储像素点的颜色值，用于合成多幅图像。产生反锯齿，反走样等内容。

消隐操作

消隐：决定场景中哪些物体可见，哪些物体被遮挡。

面剔除分析：基于面的正反面定义。

后向面判别：观察方向为V，面法向量为N，如果(V * N > 0)，则是后向面，不可见。

后向面判别是在深度测试之前进行，可以减轻计算压力。

深度测试算法：

  • 深度缓冲器算法 Z-buffer：对每个像素点找到距离视点最近的片元，也就是最靠近屏幕的片元。
    • 步骤：
      • 初始化：将深度缓存与帧缓存中所有的单元(x, y)初始化：
        • 深度缓存中各个(x, y)单元置为z的最大值1
        • 帧缓存中各(x, y)单元颜色置为背景色
      • 处理场景中每个多边形：
        • 计算多边形上各个点(x, y)的深度值z
          • 如果在前面，则计入深度缓存和帧缓存
  • 深度排序算法 画家算法：
    • 步骤：
      • 深度排序：将多边形按照深度优先级排序，存入队列N中，进的优先级高，远的优先级低。
      • 扫描转换：从队列N中逐个选择多个多边形绘制，由优先级低的开始绘制，逐个对多边形进行扫描转换。

在OpenGL中可以直接进行面剔除：

1
2
3
4
glEnable(GL_CULL_FACE); 
glCullFace(mode); // mode：GL_FRONT GL_BACK GL_FRONT_AND_BACK
// 深度测试默认是关闭状态，需要的时候可以打开
glEnable(GL_DEPTH_TEST);

透明处理

1
2
3
4
5
6
// 开启混合
glEnable(GL_BLEND);
// 设置混合的源和目标因子
// GL_SRC_ALPHA 从纹理对于的PNG图片获取不透明值
// GL_ONE_MINUS_SRC_ALPHA = 1 - GL_SRC_ALPHA
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);

对于不透明物体，使用深度缓冲正常绘制。
对于透明物体，需按照透明物体距离摄像头，由远到近绘制所有透明物体

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 排序
std::map<float, glm::vec3> sorted;
for(unsigned int i = 0; i < windows.size(); i++){
  float distance = glm::length(camera.Position - windows[i]);
  sorted[distance] = windows[i];
}
// 绘制
for(
  std::map<float, glm::vec3>::reverse_iterator it = sorted.rbegin();
  it != sorted.rend();
  it++)
  {
    model = glm::mat4(1.0f);
    model = glm::translate(model, it->second);
    shader.setMat4("model", model);
    glDrawArrays(GL_TRIANGLES, 0, 6);
  }

图形学进阶

PBR 基于物理的渲染方式

使用符合物理学的方式模拟光线，核心技术是BRDF(双向反射分布函数)，描述物体表面将光从任何一个入射方向到任何一个反射方向的反射特性。

常见PBR模型：

  • Lambert 漫反射模型
  • Phong 模型
  • Blinn-Phong 模型
  • 快速 Phong 模型
  • 可逆 Phong 模型
  • Cook-Torrance BRDF 模型
  • Ward BRDF 模型

其中后两项是基于物理的BRDF模型。

主要理论：

  • 次表面散射：对于半透明物体，光线射入后在其内部发生散射，最后射出物体并进入视野中产生的现象。光除了从原来的入射点射出，也有部分从内部的其他点射出。
  • 菲涅尔反射：当光经过折射率不同的界面上，会有部分光反射，部分光折射。反射部分的大小和观察角度有关，例如全反射现象。圆球上边缘的地方容易发生全反射，中间则偏透射。
  • 微平面理论：物体表面是一系列细小的，肉眼不可见的微平面构成的宏平面。整体有一个法向量N，每个微平面有单独的法向量N’，计算反射光线使用N’。实际采用NDF函数(发现分布函数 D(h) )来描述。使用方法：向NDF输入一个朝向h，函数返回朝向h的微表面占总体的比例。这样得到的高光反射是模糊的。

游戏中的渲染技术

为了提高真实感：

  • 运动模糊：通过合并有微小位移的多幅图像
  • 镜头泛光：由于透镜无法理想的聚焦而产生的辉光。

为了提高实时性：

  • 天空盒
  • 公告板：总是面向观察者，粒子效果
  • 延迟渲染
  • 层次细节

正向渲染：先进行光照计算，再进行深度测试

延迟渲染：先进行深度测试，再进行光照计算

层次细节LOD：根据距离动态的渲染不同细节的模型，合理分配渲染资源。

粒子系统

数据处理：生成顶点数据，生成绑定VBO和VAO，设置属性指针。

生成顶点数据：

  • 粒子的定义
  • 粒子的产生
  • 粒子的模拟
  • 粒子的排序

粒子的定义：

1
2
3
4
5
6
7
8
9
10
11
struct Particle{
  glm::vec3 pos, speed;
  unsigned char r, g, b, a;
  float size;
  float life;
  float cameradistance;

  bool operator<(const Particle& that) const{
    return this->cameradistance > that.cameradistance;
  }
}

粒子系统的属性：

1
2
3
4
5
const int MaxParticles = 200;
const float life = 2.0;
glm::vec3 startPos = glm::vec3(0.0f, 0, 0.0f); // 粒子起点
glm::vec3 endPos = glm::vec3(0.0f, 0, 4.8f); // 粒子起点
Particle ParticleContainer[MaxParticles];

粒子的产生：

1
2
3
4
5
6
7
8
9
10
int newparticles = deltaTime / life * MaxParticles;
for(int i=0; i<newParticles; i++){
  // 找出已经消亡的粒子，重新使用
  int particleIndex = FindUnusedPartticle();
  ParticlesContainer[particleIndex].life = life;
  glm::vec3 maindir = glm::vec3(0.0f, 10.0f, 0.0f); //  主要方向
  ParticlesContainer[particleIndex].pos = startPos + randomdOffset; // 起点
  ParticlesContainer[particleIndex].speed = (endPos - startPos) / life;
  // 产生随机颜色，透明度，大小等其他属性
}

粒子模拟：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int ParticlesCount = 0;
for(int i=0; i<MaxParticles; i++){
  if(p.life > 0.0f){
    p.life -= deltaTime;
    if(p.life > 0.0f){
      p.pos +=  p.speed * (float)deltaTime;
      // 将粒子p的位置，大小，颜色填充到数组particle_position_size_data particle_color_data中
      p.cameradistance = glm::length(p.pos - CameraPosition);
    }else{ // 如果消亡，则排序后，会被放到数组的最后
      p.cameradistance = -1.0f;
    }
    ParticlesCount++;
  }
}
SortParticles();

粒子的渲染：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
glBindVertexArray(VertexArrayID);
for(i=0;i<ParticlesCount;i++){
  shader.setVec4("xyzs", 
    particle_position_size_data[4*i+0],
    particle_position_size_data[4*i+1],
    particle_position_size_data[4*i+2],
    particle_position_size_data[4*i+3],
  );
  shader.setVec4("color",
    particle_color_data[4*i+0],
    particle_color_data[4*i+1],
    particle_color_data[4*i+2],
    particle_color_data[4*i+3],
  )
  glDrawArrays(GL_TRIANGLE_STRIP, 0, 4);
}

公告板技术：根据粒子中心在世界的坐标，以及相机的Up和Right向量，计算粒子的4个顶点坐标，使其始终面向摄像机。

1
2
3
vec3 vertexPosition_worldspace = particleCenter_worldspace 
  + CameraRight_worldspace * particleSize
  + CameraUp_worldspace * particleSize;